КОСИНУС - ЕВРЕЙ, или как объяснять тригонометрию в 10 классе, если все совсем плохо
Заголовок - интересный, история - забавная.
Несколько лет назад, готовились мы к ЕГЭ по математике с прекрасной девочкой Ксюшей. Ей тяжело в моменте давались такие понятия, как четная и нечетные тригонометрические функции.
Я, не долго думая, привела ей аналогию, которая помогла ей в дальнейшем. Рассказав этот пример пару раз своим ученикам и получив от них положительные комментарии, я решила рассказать всем. Итак, приятного прочтения, вдруг кому-то будет полезно.
Все мы знаем (некоторые забыли, но стоит вспомнить уж ради такой истории), что тригонометрические функции бывают четными и нечетными: Функция y = f(x) называется чётной, если её область определения симметрична относительно нуля и для любого x из её области определения выполняется равенство f(-x) = f(x). График чётной функции симметричен относительно оси ординат. Функция y = f(x) называется нечётной, если её область определения симметрична относительно нуля и для любого x из её области определения выполняется равенство f(-x) = -f(x). График нечётной функции симметричен относительно начала координат.
Звучит слегка нудно и непонятно, но это математика, что уж поделать.
Так вот, косинус - это четная тригонометрическая функция, которой без разницы, что у него стоит в качестве аргумента, он может работать и с положительным и с отрицательным одинаково. А синус, тангенс и котангенс - нечетные, и с минусом они работать не умеют, выносят его вперед перед функцией.
Кажется, ну вот что тут такого сложного и страшного, запомни, да работай. И тут в историю врывается мозг ребенка, который отказывается усваивать информацию именно в этом моменте. На помощь к нему, приходит история-аналогия.
Синус, тангенс и котангенс - это обычные среднестатистические жители вселенной математики. Они получили счета на оплату или дошли до отрицательного баланса на проездном и пошли оплачивать, тем самым устраняя минус в аргументе своей функции, вынося его вперед. Косинус же, не простой житель, а еврей. Все мы знаем, что евреи очень щепетильно относятся к своим финансам (количество анекдотов не пересчитать по всему интернету) , поэтому у косинуса нет расходов, он любые минусы у аргумента превращает в плюсы и продолжает радоваться жизни.
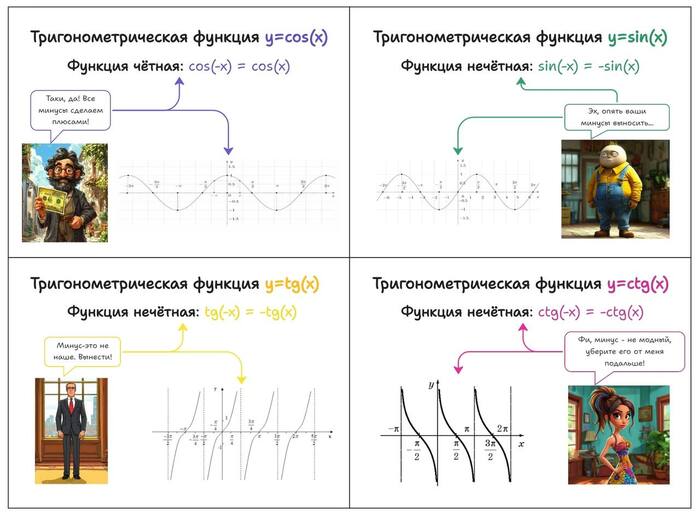
Картинка с кратким описанием прилагается, спасибо за внимание!