DELETED

Алгебра говорит ДА.⁠⁠

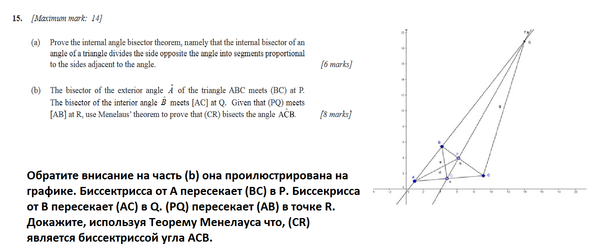
При помощи элементарных манипуляций с Менелаусом и теоремой биссектрисы треугольника, можно доказать, что CR действительно является биссектрисой к С.

(RA/RB)*(BP/PC)*(CQ/QA)=-1

по теореме биссектрис: CR должно делить AB как (AR/RB)=(CA/CB) (доказать)

BQ делит AC как (AQ/QC)=(BA/BC)

AP делит BC как (BP/PC)=(AB/AC)

отсюда: (BP*CQ)/(PC*QA)=(RB/RA)

(AB*BC)/(AC*BA)=(RB/RA) >>> (BC/AC)=(RB/RA)

Доказано, что (CR) это биссектриса к С.