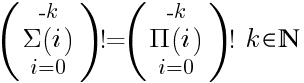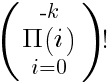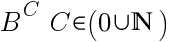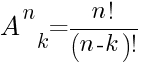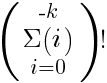Упоротые расчёты - вглядываясь в пустоту
Всем привет! Сегодня у нас на хирургическом столе вот такое математическое выражение:
Действительно ли это равенство? Как думаете? (пишите в комментариях, а ниже разберем что это).
Сама идея данного поста навеяна мне неким обсуждением в интернете (ссылка на него будет ниже). Давайте по порядку, немного определений:
Математическое множество - набор, совоку́пность каких-либо (вообще говоря любых) объектов — элеме́нтов этого множества
Подмножество - множество А, полностью входящее во множество В.
Пустое множество - множество, не содержащее ни одного элемента. При этом пустое множество является подмножеством любого множества (даже самого себя)
И вот, вооружившись такими определениями, давайте, разберëм выражение.
Правая часть
Здесь - произведение элементов некоторого множества, но само множество задано, как пустое (i должно только возрастать до числа, указанного над символом "П", которое является мерой общего количества множителей, но у нас это значение задано меньшим, чем первое порядковое). Таким образом, множество не содержит ни одного элемента, это произведение элементов пустого множества (сам способ задания пустого множества именно так я понял совершенно случайно, когда работал с формулой, в которой количество элементов было n - m, и иногда выходило m > n).
На всякий случай - привожу ниже страничку из Википедии. Итератор в суммах и в произведениях не может уменьшаться, из этого следует, что верхняя граница не может быть меньше нижней ("инкременентируется" - увеличивается)
- возведение в степень
В самом деле, число С показывает, сколько раз мы должны умножить В само на себя. И, если С=0, то любое число, возведëнное в нулевую степень, равно 1.
В^3 = B*B*B
В^0 = 1
Так, произведение элементов пустого множества равно 1
- факториал
Перед вами формула из комбинаторики - размещение k элементов из множества n. Если n=k (то есть мы заберем все элементы из множества), то количество размещений равно n! (попросту все возможные перестановки n элементов). Очевидно, что факториал разности в знаменателе нашей дроби 0! равен 1.
Факториал обозначает, что все натуральные числа от 1 до обозначенного нужно перемножить. Например:
3! = 1*2*3
7! = 1*2*3*4*5*6*7
В данном случае мы определяем некоторые натуральные числа для перемножения, их множество. А если множество пусто (как может получиться в формуле размещения), то такое произведение элементов пустого (не содержащего ничего) множества равно 1.
Левая часть
Здесь мы видим сумму элементов некоторого множества, пустого, задано оно, как и в правой части. Немного математически пофилосовствуем чему может быть равна такая сумма:
- операция умножения
Отлично показывает нам, чему равна сумма элементов пустого множества, давайте посмотрим:
A x 5 = A + A + A + A + A
Умножая число на другое число, мы производим операцию сложения этого числа (А) необходимое количество раз (то есть формируем конечное множество, в котором все элементы одинаковы, если нет дробей).
Но если во множестве, состоящем из А, нет ни одного элемента (мы на ноль умножили) - тогда наша сумма будет равна 0.
Мне прямо понравилось, как об этом написано здесь.
Действительно, ведь пустое множество это, во-первых, ничто, а во-вторых - то, что входит во все остальные множества, как полмножество. Тогда, получается, складывая элементы множества, например, простых чисел (2+3+5+7+...), мы учитываем и пустое множество с его элементами, которое не должно влиять на общую сумму (как метко выразились, быть "нейтральным"). То же верно и для умножения, 1 не влияет на общее произведение.
В итоге, получается, что тождество верно. И в левой части, и в правой мы получаем 0! = 1!
Р.S. Ссылка на то самое обсуждение: https://dxdy.ru/topic41662.html
P.S.-2 В прошлый раз сработало: Данный пост написан, чтобы немного поломать голову. Люди с особой чувствительностью, которые заявят об этом в комментариях, будут помещены в особых список чувствительных людей после моего ответного сообщения "Ваше мнение итить-колотить как важно для меня".