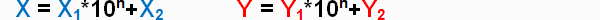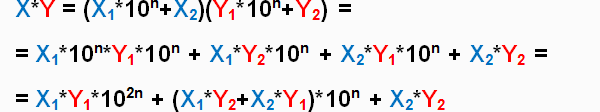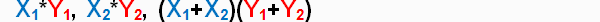Метод быстрого умножения Карацубы
Приветствую, пикабушники.
На Пикабу периодически всплывают посты вроде этого или этого, объясняющие, как якобы быстро перемножать целые числа. Но на деле они либо применимы для очень узкого класса чисел, либо медленнее даже умножения в столбик. В этом посте я постараюсь на пальцах рассказать, как действительно быстро перемножать больше числа. Сразу оговорюсь, что на практике вы этот метод вряд ли когда-нибудь примените, и пост имеет скорее познавательный характер. Итак,
Для начала нужно прояснить пару моментов.
1. Что сложнее: сложение или умножение? Ответ очевиден - умножение. Хотя бы потому, что при умножении нужно применять сложение, причем не один раз. Именно поэтому при оценивании сложности алгоритма будем считать только количество умножений, а влияние количества сложений будем считать несоизмеримо малым.
2. Как зависит сложность умножения от количества цифр в числе? Разберем этот вопрос пошагово.
2.1. Умножение однозначных чисел. Для этого нужно знать таблицу умножения. Будем считать, что это просто, и условно обозначим сложность числом 1.
2.2. Умножение n-значного числа на однозначное. Для этой операции нужно n раз перемножить однозначные числа (плюс сложения, но их мы решили не учитывать). Значит, это в n раз сложнее, чем 1, то есть сложность можно обозначить n*1 = n.
2.3. Умножение n-значных чисел. Если умножать в столбик, то это в n раз сложнее, чем предыдущий случай, т.к. его нужно применить n раз. Итого получаем n*n = n^2.
Теперь перейдем к самому методу. Для удобства будем рассматривать числа длины 2n (если количество цифр в числе нечетно, можно просто приписать слева 0). При умножении в столбик получим сложность (2n)^2 = 4n^2.
Разобьем перемножаемые числа посередине на два числа длины n:
Тогда сами числа можно записать в следующем виде:
Распишем подробно их произведение:
Напомню, что умножение на степень десятки осуществляется простым приписыванием справа нулей в количестве равном степени, а значит в подсчете сложности может не учитываться. Итого получаем, что нужно посчитать следующие 4 произведения n-значных чисел:
Каждое из них считается со сложностью n^2, всего их 4, а значит суммарная сложность 4n^2. То есть мы другим путем получили уже полученный ранее результат.
Теперь мы подошли к самой сути метода быстрого умножения. Вместо этих четырех произведений А. А. Карацуба предложил вычислять следующие три:
Как с их помощью вычислить нужное нам произведение? Первое и последнее слагаемые из полученной выше формулы и так вычисляются, осталось среднее. Вычтем из последнего произведения первые два:
Раскрывая скобки, получим в чистом виде среднее слагаемое, при этом дополнительно мы использовали лишь операции сложения и вычитания. То есть нам удалось сократить сложность с 4n^2 до 3n^2.
Теперь вопрос: как вычислять эти три произведения? Ведь если у нас были 100-значные числа, то мы получили 50-значные, а их тоже вычислять довольно сложно. Ответ напрашивается сам: точно так же! Мы повторим ту же процедуру для половинок чисел, тем самым снизив и сложность их перемножения с n^2 до меньшего значения. Таким образом, можно рекурсивно применять метод, остановившись на однозначных числах, которые уже перемножаются просто.
Не буду вдаваться в подробности вычислений, а скажу лишь, что с помощью этого метода сложность умножения n-значных чисел снижается с n^2 до примерно n^1,585 или, если быть точным, то до
Можно условно сказать, что аргумент логарифма отвечает за количество умножений на каждом шаге. Например, в случае умножения в столбик у нас было 4 умножения, и мы получали следующее:
То есть в точности тот результат, который мы получили ранее. В случае умножения Карацубы у нас 3 умножения, что и видно в формуле.
Историческая справка.
В 1956 году один из ведущих математиков XX века А. Н. Колмогоров высказал гипотезу, что не существует метода умножения чисел со сложностью менее n^2. Основана она была на том, что исторически до нас дошел метод умножения столбиком, сложность которого именно n^2. Ведь, если бы существовали методы проще, то за тысячелетия существования арифметики они бы уже были открыты. Однако в 1960 году студент мехмата МГУ А. А. Карацуба нашел метод, который я грубо изложил в этом посте. Сам Карацуба был очень скромным, и, прежде чем представить этот метод, долго просил своих товарищей найти у него ошибку. Однако мало того, что ошибка не была найдена, благодаря его открытию еще и был создан новый раздел вычислительной математики - теория быстрых алгоритмов. На настоящий момент уже найдены еще более быстрые методы умножения, однако они все несоизмеримы с тем вкладом, который сделал Карацуба.
Материал, изложенный в посте, был прочитан год назад на факультете вычислительной математики и кибернетики МГУ на лекции по дискретной математике профессором В. Б. Алексеевым и только что воспроизведен мной по памяти (за исключением исторической справки, ее я частично подсмотрел в Википедии с:).