Элементы абстрактной алгебры. Часть II. Виды отображений.⁠⁠

И снова привет. Сегодня мы поговорим о видах отображений. Надеюсь, пост https://pikabu.ru/story/yelementyi_abstraktnoy_algebryi_chas... был усвоен.

P. S. Не стоит ограничивать отображения числовыми функциями: им от этого обидно. Например, соответствие между множеством всех когда-либо живших людей и множеством родителей (тут упорядоченные пары) будет отображением.

Общий взгляд на отображение

Какими бывают отображения? Совершенно разными. Вот вам числовые функции, которые делятся на линейные, квадратичные, ...; вот вам соответствие между людьми и их родителями; вот вам движение плоскости (поворот, отражение от оси, например); вот вам гомеоморфизм двух топологических пространств, изоморфизм групп. Огромный списочек. Но есть кое-что, что выделяет некоторые отображения из всех. Классификация такова: сюръекции, инъекции, биекции и всё остальное.

Сюръекция

Определение. Отображение f множества A на множество B называется сюръективным, если для каждого элемента из B найдётся хотя бы один прообраз в A.

Чёйта такое? Это легко пояснить на схемах со стрелочками. Итак, нарисуем множества A и B

Точечки - это элементы соответствующих множеств.

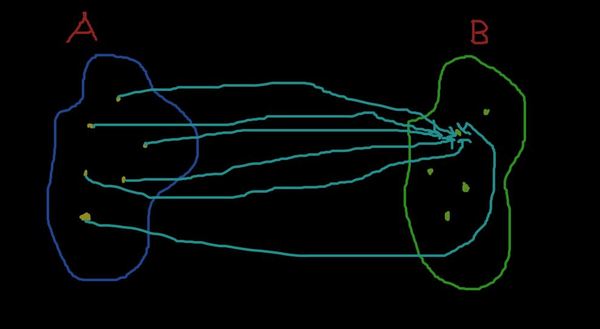
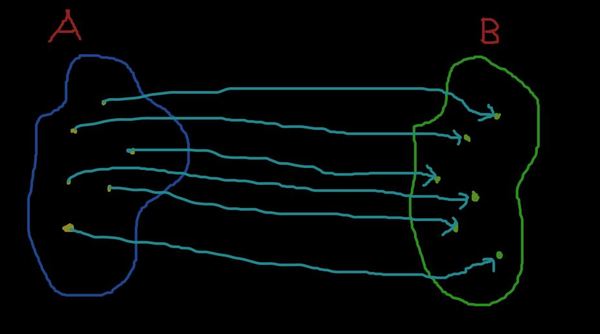
Зададим отображение множества A на B. Оно будет ставить каждой точечке из A какие-то точечки из B. Как всё это может выглядеть? Ну, например, так

Все точки из A превратились в конкретную точку из B. Кстати, такое отображение называется постоянным.

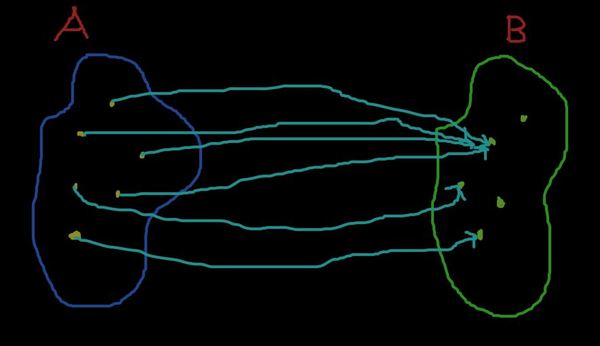
А может быть и так

И так далее.

Всё это примеры различных отображений A в B (кстати, такая схема - один из способов задания отображения). Что их объединяет? То, что во множестве B остаются "обеделённые" элементы, элементы без стрелочек, без прообразов в A.

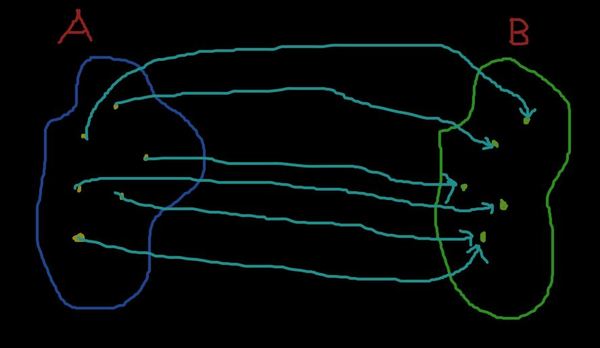
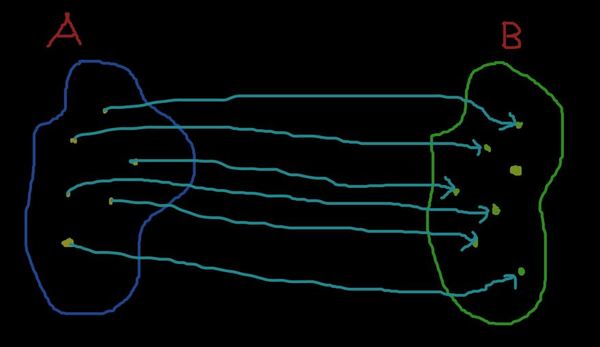
Давайте исправим ситуацию и наделим все точки прообразами в A.

Шедевр. Теперь каждый элемент в B имеет прообраз в A! И, конечно, это свойство нашего отображения (именно оно диктует, кто и какой будет иметь прообраз). А теперь посмотрите определение сюръекции и заметьте, что наше некое отображение суть пример сюръекции!

Нижняя точка выделяется тем, что имеет два прообраза в A (в неё входят две стрелочки). Это тоже особенность отображения. С тем же успехом мы можем взять одну стрелочку из нижней точки и перетащить её в верхнюю. Тогда, разумеется, получится новая сюръекция.

Давайте добавим ещё примеров.

Числовая функция f(x) = x, отображающая R на R, суть сюръекция.

Отображение g множества трёхзначных чисел на множество цифр от 0 до 9, ставящее в соответствие трёхзначному числу его 2-е число (в середине которое), суть сюръекция. Действительно, для каждого числа от 0 до 9 найдётся некоторое трёхзначное число. Например, для 1 можно найти 119, 118, 610 и так далее.

Но найти сюръективное отображение одного множества на другое не всегда возможно. Давайте отныне договоримся (это не касается примеров), что мы будем рассматривать конечные множества.

Пусть A - некоторое множество. Тогда под n(A) мы будем понимать его мощность (число его элементов). Если, например, A суть множество моих девушек, то, конечно, n(A) = 0 - оно пустое. Вот такой я хикка.

Итак, между двумя множествами A и B можно установить сюръективное отображение тогда и только тогда, когда n(A) >= n(B).

И вправду. Если n(A) < n(B), то у нас просто не хватит элементов в A, чтобы занять все точки в B стрелочками.

Инъекция

Ясно, что покуда n(A)> n(B), мы не сможем напихать стрелочки так, чтобы элементы в B имели только один прообраз в A (не обязательно все элементы = это не обязательно сюръекция). У нас просто в A будет избыток стрелочек!

Давайте посмотрим на случай n(A) = n(B).

Среди всех возможных отображений выделяется один класс отображений, который выглядит так

Красиво! Элементы в B имеют ровно один прообраз в A. Никаких избытков стрелочек, все равноправны, всё по Марксу-Энгельсу.

Посмотрим на n(A) < n(B). В таком случае мы всегда сможем установить отображение, которое элементам из B даёт ровно по одному прообразу в A. Правда, тут уже будут не все точки заняты (то есть это не сюръекция), но всё же.

Короче говоря, разные элементы A переходят в разные элементы B (имеют разные образы при отображении).

Определение. Отображение, при котором разные элементы отображаемого множества имеют разные образы, называется инъекцией.

Разумеется, на неё тоже имеются ограничения по мощностям множеств, а именно: n(A) =< n(B).

Упражнение 1. Доказать это.

Примеры валяются под ногами. Если у нас есть команда футболистов, то на их майках имеются номера. Соберём все номера во множество номеров. Очевидно, можно установить инъективное отображение множества номеров на множество игроков футбола в данном конкретном матче.

Биекция

Определение. Если отображение одновременно инъективно и сюръективно, то оно называется биекцией.

Иначе говоря, мы имеем биекцию, когда нет избытка стрелочек и заняты все точки (имеются пары точек). Картинка оной была выше, когда смотрели на n(A) = n(B)

Упражнение 2. Докажите, что между двумя множествами можно установить биекцию тогда и только тогда, когда n(A) = n(B).

Соберём всё воедино.

Отображения делятся на сюръекцию, инъекцию, биекцию и всё остальное. Сюръекцию имеем тогда, когда каждый элемент из "второго" множества имеет прообраз в отображаемом множестве, при этом обязательно n(A) >= n(B). Инъекцию - когда разные элементы A переходят в разные элементы B, при этом обязательно n(A) =< n(B). Биекцию - когда образ и прообраз образуют пару, когда отображение суть инъекция и сюръекция, при этом обязательно n(A) = n(B).

Я часто подчёркивал "отображение на" и "отображение в". Настало время это прояснить.

"Отображение на" - это сюръекция и биекция.

"Отображение в" - инъекция и всё остальное.

Вот так. :^)

Упражнение 3. Написать в комментарии по 3 примера на каждое отображение (не забудьте про "все остальные отображения"!).