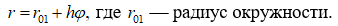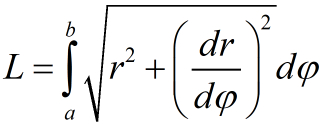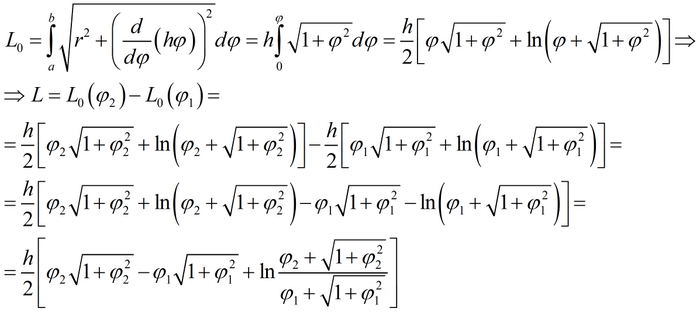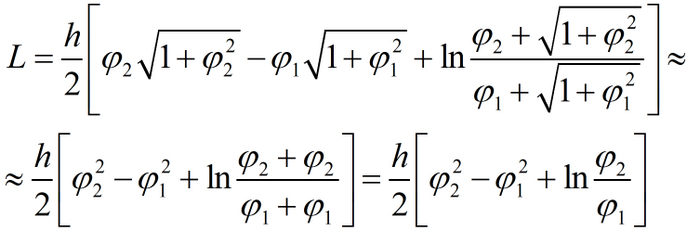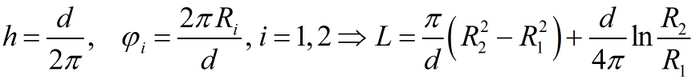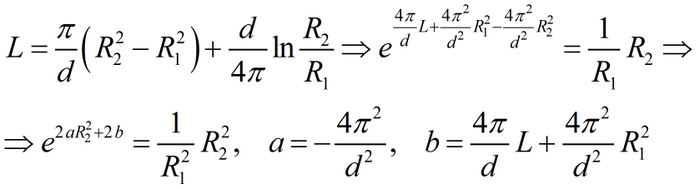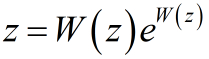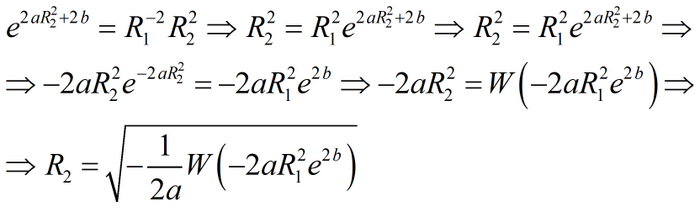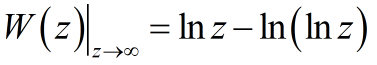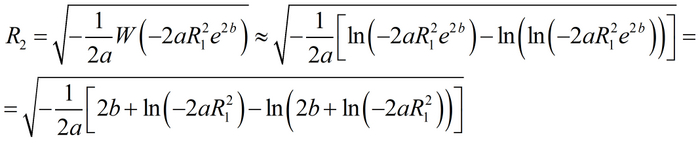Это были упоротые измерения, а хотелось бы упоротый расчёт. Ну, там, исходные данные - толщина бумаги, внешний и внутренний диаметр рулона. Методика, формулы, интегрирование, ряд Фибоначчи и так далее. То, что все в школе проходили, но уже забыли.
Итак, поперечное сечение рулона, как правило, описывается спиралью Архимеда. При этом ставится условие, что поперечное сечение втулки является окружностью, а зазоры между витками отсутствуют. Следует отметить, что спираль Архимеда не обладает постоянным шагом, если под этим понимать длину отрезка нормали к любой паре соседних витков в любой точке. Иными словами, если записать уравнение спирали Архимеда как:
то задействовав переход к декартовым координатам с последующим вычислением тангенса угла наклона касательной (производная), получим, что:
Разрешением этого обстоятельства было бы использование кривых Бертрана или в данном случае, учитывая фактор плоской задачи, эквидистантные кривые, но в первом приближении забьём на это обстоятельство и поработаем с Архимедом.
Длина полотна в рулоне (при соблюдении различных условий) или в данной задаче длина спирали Архимеда рассчитывается по известной формуле:
Как же неудобно оформлять, но ладно.
Обратим внимание, что в нашем варианте уравнения спирали имеется постоянный член, грубо говоря, отвечающий за наличие втулки. Упростим расчёты с аргументацией типа "она и так не является параллельной, что нам эти дельты по переменным в точке перехода ловить?", для чего установим следующий подход к вычислению длины:
Задать радиус втулки,
Задать внешний радиус рулона,
Найти длину спирали Архимеда для обоих радиусов,
Подсчитать разность.
В таком случае, получим следующую формулу:
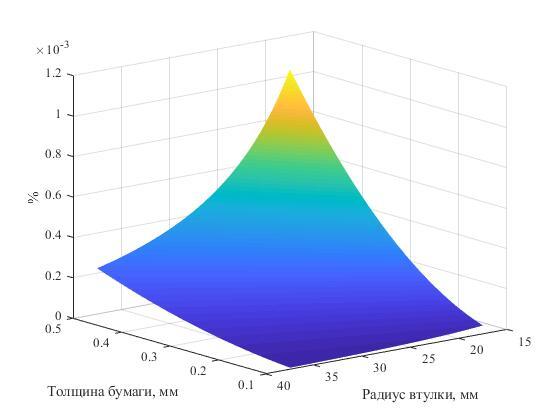
Славная формула, но вдруг можно упростить? Согласно быстро найденным данным, примем толщину бумаги, то есть шаг спирали, равным 0.1 мм (шаг спирали равен 2*pi*h). Зададимся диаметром втулки, равным 35 мм, в таком случае для первого угла получим значение примерно 1100 рад. Это значение отличается от sqrt(1100^2+1) примерно на 4.55e-4, что составляет не более 0.000042% от 1100. Нетрудно догадаться, что для большего радиуса разность станет ещё меньше. В противовес можно заявить о толщине бумаги, но строить поверхность разностей в зависимости от толщины бумаги и радиуса... будем.
Есть начало обоснования в пользу упрощения выведенной ранее формулы. Искать ещё аргументацию не будем кто как хочет, хех. Упростим формулу длины:
Перейдём к радиусам и введём переменную d, являющуюся толщиной бумаги. После упрощений получим:
Итак, по этой формуле можно оценить длину бумаги в рулоне. Отметим, что некоторые онлайн калькуляторы рулона используют эту формулу без второго слагаемого, что в ряде ситуаций обосновано. Например, для рулона офсетной бумаги с внешним диаметром 1000 мм, диаметром втулки 76 мм и толщиной 100 мкм, второе слагаемое равно примерно 0.02 мм.
Обратимся к первому слагаемому. Нетрудно заметить, что определение длины через него фактически базируется на представлении поперечного сечения рулона как множество концентрических окружностей и том факте, что с ростом количества витков форма внешнего витка спирали всё больше приближается к окружности (доказывается тривиально, достаточно рассмотреть отношение минимального и максимального расстояния от центра до витка).
Несложно вывести обратную формулу, то есть расчёт внешнего радиуса рулона в зависимости от длины. Для формулы только с первым слагаемым всё довольно просто, для двух слагаемых необходимо выполнить некоторые преобразования:
Полученное уравнение относительно R2 является трансцендентным, то есть оно не алгебраическое. И тут на сцену выкатывается тяжёлая артиллерия в виде W-функции Ламберта, позволяющей записать решение некоторого множества трансцендентных уравнений. Она определяется через функциональное уравнение следующим образом:
Используем её для нашего уравнения, для чего выполним преобразования:
Надо отметить, что если аргумент W-функции окажется большим, то имеет смысл задействовать асимптотику функции.
В сущности, всё зависит от коэффициента b. В результате получим следующее:
Вот это уже пойдёт. Пример. Воспользуемся онлайн калькулятором и зададим внутренний диаметр (втулка) 35 мм, внешний — 90 мм, а толщина равна 100 мкм. Сайт даёт длину, равную 53.99612373 м (следует отметить, что как раз один из найденных онлайн калькуляторов посчитал по упрощённой формуле без слагаемого с логарифмом). Применим обратную формулу и найдём модуль разности между исходным значением внешнего радиуса и рассчитанным. Получим достаточно малую величину 5.3189e-06 мм. Расчёты подтвердились.
Формулы красивые, выводил их (по расчёту радиуса от длины) лет десять назад. Всем раздать формулы.
Интеграл хороший. Канал не веду, так что в телеграм не приглашаю.
P. S. Всем качественных рулонов и да прибудет с вами сила математики.
P. P. S. Можно, конечно, построить куда более сложную модель и развлекаться там. Пс-сс, как насчёт задания толщины бумаги как стохастической функции и расчётов плоскопараллельной задачи из области сопромата?