Всего лишь несколько столетий назад считалось, что Земля неподвижна, а Солнце и планеты вращаются вокруг неё. Теперь мы знаем, что именно планеты движутся вокруг Солнца. Про нашу планету обычно говорят, что вокруг неё вращается Луна, а сама Земля движется вокруг Солнца. Однако правильнее говорить, что вокруг Солнца движется центр масс системы Земля–Луна, при этом и Земля, и Луна вращаются вокруг их общего центра масс.

Видео показывает, как наша планета в процессе движения вокруг Солнца колеблется относительно общего центра масс с Луной. Период колебаний Земли вокруг этого барицентра совпадает с периодом вращения Луны вокруг него же и составляет 27.3 дня. Пока вы “неподвижно” читаете этот текст, вы на самом деле движетесь вокруг Солнца по очень сложной траектории. Находясь на поверхности Земли, вы делаете оборот вокруг её оси за одни сутки. При этом вы совершаете колебания относительно барицентра Земля–Луна примерно за один месяц и делаете оборот вокруг Солнца за один год. Барицентр находится внутри Земли, то есть радиус колебаний несколько меньше радиуса самой планеты. Луна при этом движется вокруг барицентра по аналогичной траектории. Но эта траектория зеркально отражена и больше по размерам во столько же раз, во сколько масса Земли больше массы Луны.

Видео также наглядно показывает явление прецессии орбиты Луны. Прецессия заключается в медленном повороте эллипса лунной орбиты в пространстве за 8 лет и 10 месяцев. Плоскость орбиты Луны также поворачивается и делает полный оборот примерно за 18 лет и 7 месяцев. Лунная прецессия возникает в первую очередь из-за того, что на Луну, помимо гравитации Земли, действует гравитация Солнца. Причём гравитация Солнца, действующая на Луну, более, чем в два раза превышает гравитацию Земли. Помимо Солнца вклад в прецессию лунной орбиты также вносят формы Земли и Луны, отличные от сферической. Прецессия лунной орбиты объясняет цикличность солнечных затмений. При этом Луна постепенно удаляется от Земли примерно на 3.8 метра за столетие. Это приведёт к тому, что примерно через 750 млн лет наблюдать полные солнечные затмения с поверхности нашей планеты станет невозможно…

На протяжении части этого видео размеры Земли, других планет, Солнца и Луны показаны сильно преувеличенными по сравнению с расстояниями между телами. Скорость вращения Земли вокруг своей оси показана значительно уменьшенной по сравнению со скоростью движения небесных тел по своим орбитам.

Моделирование и визуализация выполнены автором этой публикации с помощью программного обеспечения собственной разработки. При расчетах учитывалось взаимное влияние друг на друга Солнца, всех планет Солнечной системы и Луны. Также при расчете учитывались релятивистские эффекты.

Нетрудно заметить, что центр масс планет всё время находится неподалёку от Юпитера. Это связано с тем, что масса Юпитера почти в 2.5 раза превышает массу всех остальных планет вместе взятых. При этом центр масс смещён в сторону окольцованного Сатурна, который является вторым по размерам и массе среди планет Солнечной системы. Видео показывает, что этот центр масс не лежит на отрезке, соединяющем Юпитер и Сатурн. Он несколько смещён в сторону в зависимости от положения Урана и Нептуна на своих орбитах. Внутренние планеты (Меркурий, Венера, Земля и Марс) на его положение влияют крайне незначительно.

В апреле 2023 года было опубликовано видео, показывающие движение Солнца относительно центра масс всей Солнечной системы, который находится рядом с Солнцем, потому что именно в звезде сосредоточена подавляющая часть массы всей системы. По сути траектория Солнца относительно центра масс всей Солнечной системы совпадает с траекторией, показанной в этом видео. Только она зеркально отражена и меньше по размерам во столько же раз, во сколько раз Солнце массивнее всех остальных планет вместе взятых.

Иногда центр масс планет проходит очень близко к Солнцу. Это случается, когда Юпитер и Сатурн оказываются по разные стороны от Солнца. Одно из наиболее интересных прохождений центра масс планет вблизи Солнца произойдёт в феврале 2169 года. Все планеты выстроятся практически в одну линию, что случается чрезвычайно редко. Свидетелями этого события станут наши потомки…

Моделирование и визуализация выполнены автором этой публикации с помощью программного обеспечения собственной разработки. При расчетах учитывалось взаимное влияние друг на друга Солнца, всех планет Солнечной системы и Луны. Также при расчете учитывались релятивистские эффекты.

Именно при таком законе тяготения мы можем наблюдать привычные нам орбиты (эллипс, гипербола, парабола). Но что, если бы закон был немного другим, как бы тогда выглядели орбиты?
На это мы сейчас и посмотрим. Ну а самый удобный способ посмотреть на ньютоновскую гравитацию - нарисовать орбиты, поэтому именно так будем определять, что было бы, если бы гравитация работала по-другому. А заодно вы сможете сами и без математики покрутить и повертеть эти орбиты, в конце поста оставлю файл и инструкцию к нему

Ну и оставлю небольшое уточнение перед прочтением: во всех случаях коэффициенты подобраны так, что сохраняется ускорение свободного падения на Земле (а не ее масса). Сделал это для удобства, иначе была бы куча мучений со скоростями). Ну и да, орбиты вокруг Земли, хотя это не особо важно

Что будем менять в гравитации?

Прежде чем начать смотреть на красивые графики и страшные формулы, разберемся, что мы вообще хотим поменять. Ну, очевидно, не гравитационную постоянную, ведь принципиально от этого ничего не изменится. Также очевидно, что и не степени или коэффициенты при массах, так как в таком случае мы по сути будем просто менять константы при формуле, опять-таки, принципиальной разницы не будет
Однако, если менять степень при расстоянии, то вот тогда мы получим принципиальные различия. Ведь сменой степени мы по сути поменяем и характер уравнений, описывающих движение (что будет видно дальше)
Замечу, что еще можно не только что-то менять в самой формуле, но и дополнять ее. Однако способов ее дополнить в значительно раз больше, чем способов изменить, поэтому на все подобные дополнения поста уж точно не хватит. Так что введение чего-то нового в формулу оставлю читателям в качестве упражнения)

Немножко про обычный закон тяготения

Но начнем мы все таки с того, как и почему возникают привычные нам формы орбит. Тут на самом деле все довольно просто, но, как мне кажется, будет полезным показать, как все это дело получается. Записываем уравнения движения в полярной системе координат и решаем их:

Полученное уравнение, хоть это и не выглядит очевидным, описывает кривые второго порядка с фокусом, лежащим в начале системы координат. То есть мы получаем наши привычные эллипсы, гиперболы, параболы (ну и окружности с прямыми). Покрутить их можно здесь. А, ну и пару картинок, как полагается:

Еще один частный случай закона тяготения

Помимо случая с квадратом радиуса есть еще один вариант, для которого можно решить уравнения движения - кубическая зависимость от расстояния. Правда, здесь решение будет более громоздким, поэтому часть выкладок, использованных выше, я опущу:

Во всех трех случаях (кроме 2 при нулевой вертикальной скорости) формулы задают спирали (видно на картинке ниже). Первая, с экспонентами, и вторая при направленной вниз вертикальной скорости дают спирали, которые стремятся к центру планеты (1 и 2 на картинке соответственно). Вторая при направленной вверх вертикальной скорости и третья дают спирали, которые наоборот "уходят" от планеты (4 и 5 соответственно). И только 2 случай при нулевой вертикальной скорости (3 на картинке) дает привычную круглую орбиту

В реальности (ну как реальности, в жизни все таки в уравнениях не куб) вероятность выпадения вот такой удобной конфигурации скоростей (скорость в точности равна первой космической и в точности направлена в горизонт) у спутников да и у чего угодно равна примерно ноль целых хрен десятых, так что с такой гравитацией появление звездных систем просто-напросто невозможно. Поэтому давайте порадуемся за квадрат в наших уравнениях, а то не видать бы нам красивых восходов и закатов, луны на небе, да и года отмерять нечем было бы, нового года бы не отмечали) Правда и отмечать было бы некому)

Ах да, покрутить такие орбиты тоже можно, вот ссыль

А что там с остальными степенями

Для всех других степеней у расстояния, увы, аналитических решений нет. Но не беда, ведь есть тяжелая артиллерия в виде численного моделирования)

К этому сейчас и приступим, но сперва пошаманим над формулами. Перепишем исходную систему в более общем виде через параметр в степени расстояния, а также перепишем систему так, чтобы заменить время на угол:

Система позволяет моделировать через время, а конечное уравнение - через угол. Пользоваться будем и тем, и тем, в зависимости от того, какая модель будет удобнее

Итак, пишем код для каждой модели

В отличие от моих предыдущих постов, где я выводил набор графиков, здесь я решил добавить ползунки и пользоваться ими. Графики кстати выглядят вот так:

Ну и теперь наконец смотрим на орбиты. Коэффициент при степени я подписал над графиками:

Вот такая красота получается. Особенно интересными графики выглядят при n > -3, образуя интересные и красивые узоры
А еще смотрите как прикольно витки орбиты "складываются" в окрестности n = -2 (привычная гравитация) и n = 1 (может получиться при привычной гравитации если лететь сквозь равномерный по плотности шар, об это рассказывал здесь):

Подметим еще два интересных факта:
1. Если буква n не меньше -1, то бессмысленно понятие второй космической, так как она будет бесконечна. Это вытекает из потенциальной энергии на бесконечном расстоянии. Проверить этот факт легко, поэтому оставлю это как еще одно упражнение для читателей)
2. Если n = -1, то первая космическая скорость будет всюду одинакова. Проверить тоже несложно, поэтому также оставлю в качества упражнения для читателей)

Как самому повертеть орбиты?

Как и обещал, оставлю модели для собственного ковыряния орбит (также можно посмотреть частные случаи в Desmos-е, дублирую ссылки [n=-2], [n=-3]). Обе численные модели вы можете скачать с ЯДиска по этой ссылке (представлены в файле формата .CDF)
Чтобы открыть их, нужно установить себе прогу Wolfram Player (ссыль на оф. сайт, она бесплатная) и запустить через нее скачанный файл
Внутри там все будет написано, так что проблем с пониманием чаво и каво возникнуть не должно. Также не бойтесь, если график становится красным или выдает ошибку, это нормально, связано с "сингулярностями" в некоторых точках при вычислении. Если возникают какие-то проблемы с моделью, либо хотите поменять границы у ползунков - пишите в комментарии, буду исправлять и дополнять. Ну и оставлю картинкой интерфейс программки:

Что по итогу?

Осматриванием прикольных картинок, ой, то есть путем сложных научных изысканий можно понять, что стоит порадоваться за наш удобный закон тяготения) Ведь при других коэффициентах звездных систем или бы не было, или Вселенная скорее всего не успела бы развиться (для n >= - 1, ну когда второй космической нет), или орбиты были бы такие, что и не разберешься, что за ужас в космосе творится (а то попробуй по тем узорчикам разбери, как гравитация устроена :) )

На такой веселой ноте пост заканчивается. Однако, помимо классического "Надеюсь, было интересно и познавательно, если что-то было непонятно - спрашивайте", хотел бы спросить у вас, как вам добавление упражнений для самостоятельного решения читателями? Мне идея показалась хорошей, так как и материал особо не выдергивается, и есть возможность читающим самим что-то дополнительно повысчитывать, и хотелось бы какой-никакой фидбэк

За сим окончательно откланиваюсь, и всем желаю удачи, счастья, успехов и нормальной гравитации в Новом 2024 году!!!

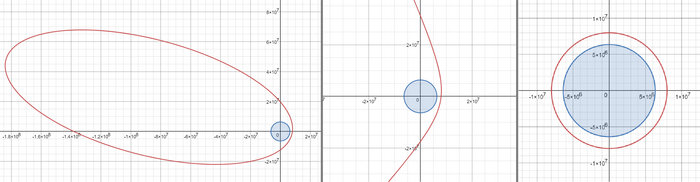
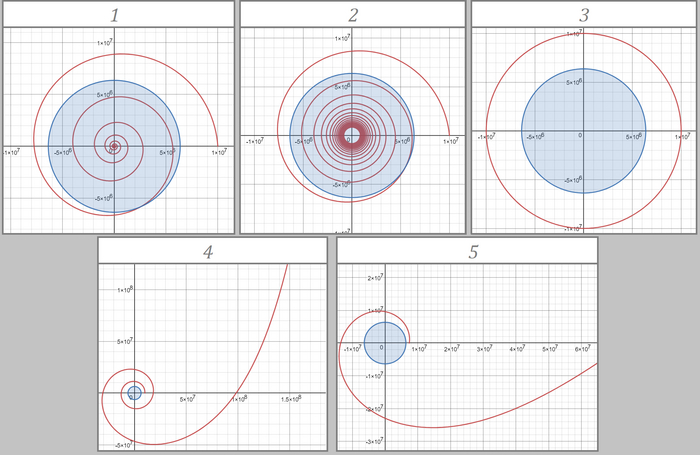
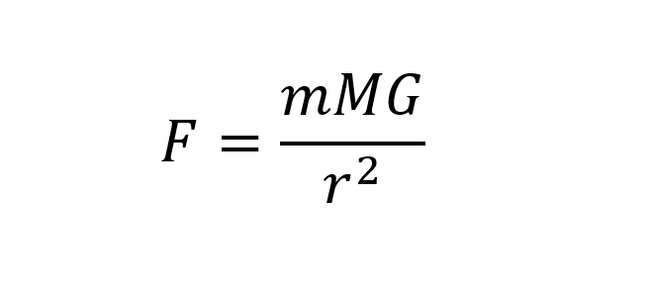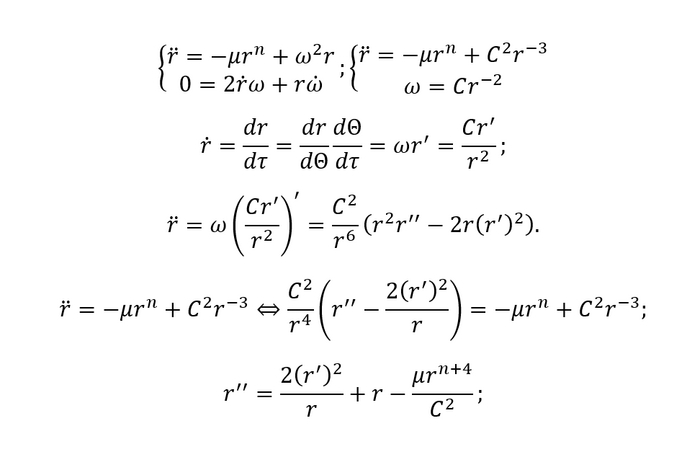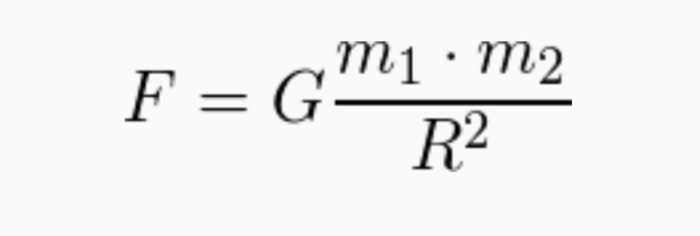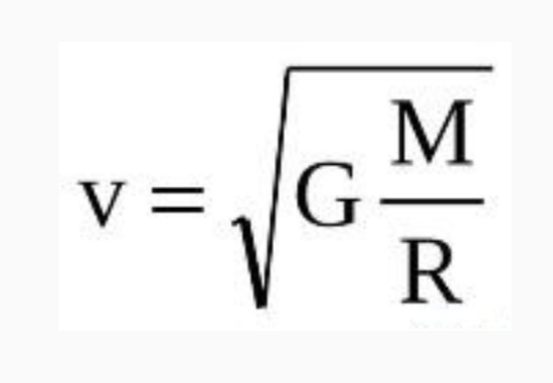В моей недавней публикации о комете Галлея проскользнула мысль о том, что основным критерием уникальности небесного тела является его орбита. Эта мысль проскочила для меня самого неожиданно — в каком-то потоковом формате, и нуждается в осмыслении.

Для моих читателей я должен кое-что уточнить.

Задавались ли Вы вопросами: "Что есть орбита, и может ли на одной орбите в один и тот же момент времени находиться более одного небесного тела?"

Для большинства людей понятие космической орбиты равно некоторой линии, чаще всего такая линия замкнутая, круглая, может быть овальная. Для астрономов понятие орбиты сложнее.

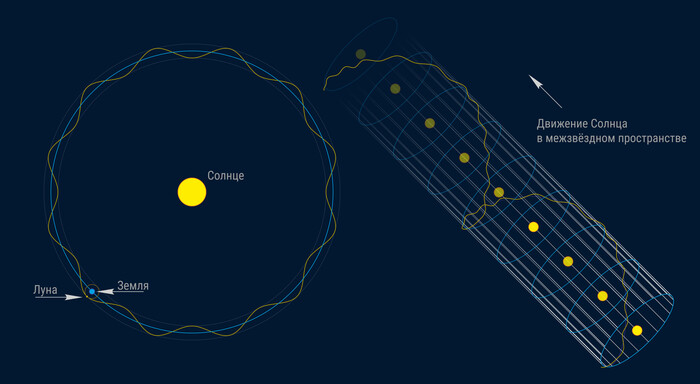
Орбита Луны в разных системах отсчета

• Во-первых, астрономы любую орбиту определяют в некоторой системе координат, и отдают себе в этом отчет, сразу допуская, что в другой системе координат эта же орбита может выглядеть принципиально иначе. Яркий тому пример — орбита Луны, которая в системе отсчета связанной с Землей является слегка вытянутым эллипсом, но с системе отсчета связанной с Солнцем она же представляет из себя волнистую змейку, словно "вьюнок" обвивающую орбиту Земли. Если оторваться от Солнца и рассмотреть орбиту Луны из системы отсчета максимально усредненной для ближайшего к нам звездного окружения, оттуда мы увидим мы увидим весьма растянутую и слегка волнистую пружинку — совершенно незамкнутую траекторию, устремленную к далеким звездам созвездия Геркулеса. Менять системы отсчета можно до бесконечности. Остановимся на той, которая для нас сейчас наиболее актуальна. И коль скоро мы говорим о телах Солнечной системы, пусть наша система отсчета будет связана с Солнцем.
  

• Во-вторых, астрономы, даже если они рисуют орбиты на листе бумаге, всегда представляют их в объеме — в 3-мерном пространстве (бумага — 2-мерное пространство). Орбиты имеют относительное наклонение — посмотришь с полюса солнечной системы — они могут совпадать, а взглянешь "с ребра" и видишь, как сильно их плоскости наклонены друг по отношению к другу.
  

• В-третьих, астрономы всегда рассматривают любую орбиту во времени, понимая, что любая орбита эволюционирует: меняется со временем тот самый наклон к плоскости эклиптики, медленно дрейфуют узлы (точки пересечения орбиты небесного тела с плоскостью эклиптики) и линия апсид (соединяющая ближайшую к Солнцу и наиболее удаленную от него точки орбиты). Фактически меняются все элементы орбиты. Происходит это из-за взаимного гравитационного влияния жителей Солнечной системы — в первую очередь наиболее массивных, таких как Юпитер, Сатурн, Уран и Нептун. Но и те, что поменьше, тоже вносят свою лепту. Важно понимать, что любая орбита определена не вообще, а лишь для некоторого момента времени. И в другой момент времени это уже немного другая орбита.
  

• В-четвертых, никакая орбита не расскажет нам о текущем положении небесного объекта, если на ней не задано отправное положение объекта на некоторый ключевой момент времени. И это исходное положение небесного тела на своей орбите фактически тоже является неотъемлемым свойством орбиты. В таблице элементов орбит планет, астероидов, комет такое опорное положение обычно указывают в самой последней графе — это эклиптическая долгота на момент T0 (раньше это было весеннее равноденствие 1950 года, потом его заменили на весеннее равноденствие 2000 года, а теперь эклиптическая долгота для T0 уточняется и указывается ежегодно — точность и значимость этого параметра растет).

Орбиты небесных тел не обязаны лежать в одной плоскости

Вот, теперь, когда мы немного прояснили понимание того, что вкладывается в понятие "орбита", давайте разберемся с тем, как астрономы отличают одно небесное тело от другого.

Конечно, Солнце с Луной не перепутаешь, но в отношении остального шанс запутаться есть.

Юпитер, Луна и Венера февральским вечером 2023 года. Как понять, что есть что?

Впервые за решение этой проблемы взялись волхвы и кудесники, жрецы и колдуны Бронзового века, когда необходимость планирования во времени стала критической, и люди обратили взор в небо за подсказками. Небосвод был разделен на созвездия, а "неподвижные звёзды" отделены от "блуждающих светил". Ярким примером путаницы была планета Венера, которая на протяжении тысяч лет воспринималась как два разных небесных объекта — “Утренняя звезда” и “Вечерняя звезда” — даже в научно продвинутой античной Элладе за 500 лет до начала Новой Эры рассматривались как два разных небесных объекта, или же как два разных божества — Эосфорос (“Свет Утренней Зари”) и Фосфорос (или Геспер — “Несущая свет”) — в зависимости от времени суток. Пифагор, вероятно, был первым, кто сумел доказать идентичность обоих объектов, но общество той эпохи (даже научное общество) к подобным прозрениям не было готово, потому что не существовало критерия, по которому можно было бы однозначно судить об идентичности небесных объектов.

Кому-то это может показаться странным — ну, неужели не ясно — вот объект был виден вечером в заре, потом он погрузился в зарю и перестал быть видимым, а через несколько дней нечто похожее на него появилось уже в утренней заре. Интуиция подсказывает, что это одно и тоже “нечто”. Но как исключить версию, что существуют два похожих, но физически раздельных объекта, которые в некоторой закономерности сменяют друг друга? Между прочим, до сих пор существуют люди, наивно верящие, что Луна (полная) и тонкий Месяц — два разных небесных тела, которые по некоторым правилам сменяют на небе друг друга, и даже в редких случаях видны одновременно.

Но если уж с Венерой и Луной возможна такая путаница, что говорить о множестве таких объектов, как астероиды и кометы, которые либо ничем не отличаются даже при наблюдении в телескоп с самым большим увеличением — звезда звездой и никаких подробностей (это астероиды, или — малые планеты), либо постоянно меняют облик: отращивают хвост, теряют хвост, распушают косматую голову, меняют яркость и в несколько ночей могут из слабого туманного пятнышка превратиться в нечто раскинувшееся на весь небосвод (это кометы). Как при этом быть уверенным, что мы видим тот же объект, который видели прошлой ночью, а не какой-то другой — просто похожий?

Венера и Меркурий при наблюдении в телескоп с увеличением около 150x

Действительно — небесные тела могут перемещаться и менять свой вид. Вид может быть обманчив. К примеру, Венеру и Меркурий нетрудно перепутать при наблюдении в телескоп — то и другое похожим образом меняет фазы, и не показывает явную детализацию поверхности. Конечно, Меркурий поменьше Венеры, но когда не можешь непосредственно сравнить, то настигает чувство неуверенности. Сатурн очень похож на Юпитер в моменты исчезновения колец (такое случается каждые 15 лет, когда кольца поворачиваются к нам ребром), и неискушенный наблюдатель запросто спутает одно с другим. Бывает очень непросто отличить Уран от Нептуна, а Уильям Гершель, когда впервые обнаружил Уран, принял его за комету — бывало и такое!

Юпитер и Сатурн (в эпоху "исчезновения колец") при наблюдении в телескоп с увеличением около 150x

И только одно знание помогает нам безошибочно определить, что перед нами именно этот объект, а не другой — это факт того, что объект находится на своей орбите, и расположен именно в той области неба, где ему и положено быть. Яркий тому пример: Нептун был обнаружен ровно на своей орбите — в той точке пространства, где и должен был располагаться, и хотя прежде его никто не видел, его положение в пространстве точно показало, что это именно та искомая планета. С Плутоном похожая история — он попал в список планет только потому, что оказался на некоторой заранее предвычисленной орбите. И вопреки своим скромным физическим свойствам он несколько десятилетий оставался в классе больших планет Солнечной системы лишь благодаря своей орбите.

"Орбита играет планету!"

Сейчас астрономы ведут поиски так называемой "Планеты X", орбита которой уже в некоторой степени определена (рассчитана Константином Батыгиным и Майклом Брауном). Осталось дело за малым — открыть физическое тело на этой орбите. Но опять орбита выступает как первичный идентификатор небесного тела — само тело еще не обнаружено, а орбита уже известна (в некотором допущении).

Майкл Браун и Константин Батыгин — ловцы Планеты X

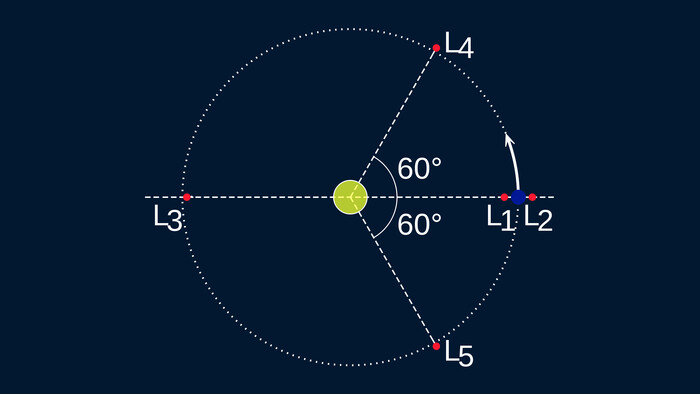
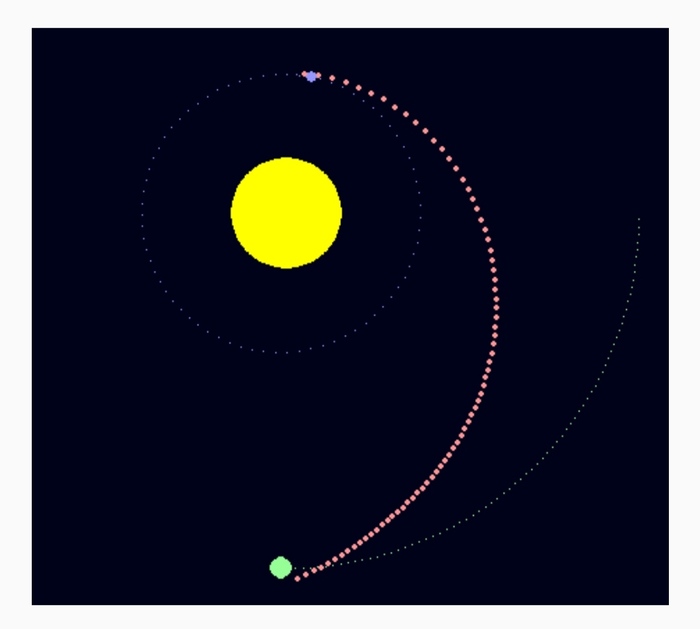
Существуют особые случаи, когда может показаться, что на одной орбите “живут” сразу несколько небесных тел. В первую очередь надо вспомнить о точках Лагранжа — в особенности о L3, L4, L5, которые на картинке лежат (в значительной точности) на орбите первичного небесного тела. Но тут важно понимать, что это только на картинке так. В реальности все те объекты, которых угораздило попасть в гравитационное равновесие точек Лагранжа участвуют как минимум сразу в двух орбитальных движениях (или их орбиты можно рассматривать как по меньшей мере два слагаемых).

Точки Лагранжа — точки гравитационного равновесия в системе двух массивных тел

Первое — их радиус вектор всегда немного больше или немного меньше радиуса-вектора "родительской орбиты" (для точек L4, L5 — чуть больше; для L3 — чуть меньше), но для астрономии все эти "немного" и "чуть-чуть" очень существенны.

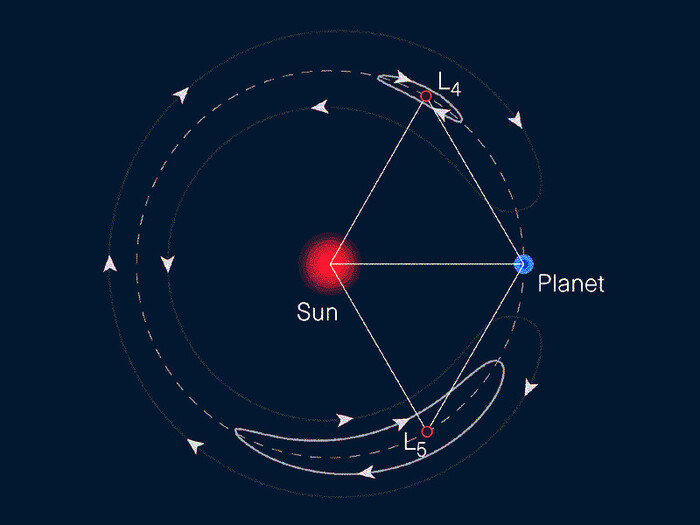
Гало-орбиты вблизи точек L4 и L5

Второе — только что речь шла о центре гало-орбиты, в котором нет ничего. Самое же тело совершает некоторое довольно сложное (можно сказать даже — диффузное — в первой степени приближения) движение вокруг точки Лагранжа. И распутывание этой траектории — это уже высший пилотаж исследования орбит небесных тел. Но без этого астрономия не была бы астрономией. Ярким примером того, насколько "глубока кроличья нора", могут служить два семейства астероидов — Греки и Троянцы. Это несколько тысяч малых планет, на первый взгляд хаотично дрейфующих вдоль орбиты Юпитера — вблизи точек L4, L5. Хаотичным их движения может показаться только на первый взгляд. Специалисты по небесной механике отлично изучили движение каждого из нескольких тысяч таких квази-спутников Юпитера. Для каждого из них определена уникальная орбита. И только благодаря точному знанию их орбит астрономы отличают одного Грека от другого, одного Троянца от такого же точно на вид, но физически отличающегося. И это настолько серьезно и прочно, что до сих пор астрономы ни разу не спутали в этих облаках из тысяч астероидов один объект с другим. Хотя по своему облику (при наблюдении с Земли) большинство из них не отличаются никак.

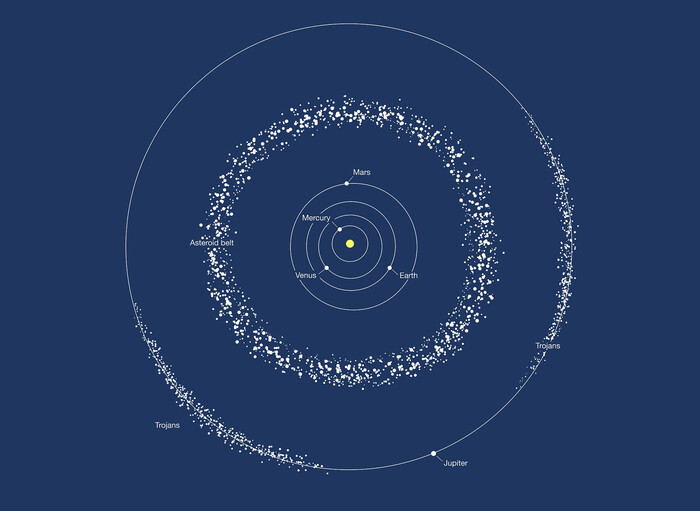
Более того, точное знание таких близких на первый взгляд орбит позволяет отправить в облако Троянских астероидов космический аппарат для их исследования. Собственно, аппарат уже запущен в 2021 году — это станция Люси, которая с 2027 по 2033 год намерена исследовать 4 астероида вблизи точки L4 системы “Солнце — Юпитер” (Греки) и два астероида вблизи точки L5 (Троянцы), которые представляют связанную гравитационную систему и обращаются вокруг общего центра масс, двигаясь каждый по своей особой орбите, что тоже учтено с самой высокой точностью, и астрономы не спутают два этих астероида, хоть их орбиты в системе отсчета связанной с Солнцем довольно близки (но все же разные).

Троянские астероиды вблизи точек L4 и L5 у орбиты Юпитера

В истории небесных тел бывали случаи, когда тела существенно меняли свои орбиты, ведь орбиты склонны к изменениям. В особенности это касается комет — кометы очень зависимы от влияния планет-гигантов. Иногда кометы попадали в плен некоторой массивной планеты и становились их спутниками. А потом вырывались из него и оказывались уже на совершенно иной околосолнечной орбите. Справедливо ли считать после таких орбитальных превращений комету той же самой?

Это вопрос открытый. Но часто при таких процессах комета терятся — астрономы ищут её на прежней орбите, найти не могут, и вход идут более глубокие вычисления, которые и показывают, что комета была "украдена", например, Юпитером. Но нельзя вот так просто всё посчитать и успокоиться. Комету обязательно надо отыскать на небе и убедиться, что расчеты верные и благодаря им комета визуально обнаружена. Если это удается, такое событие называют переоткрытием кометы.

Астрономическая история кометы начинается с открытия, и тогда она получает имя — как правило соответствующее фамилии первооткрывателя, или фамилиям, когда открыли одну и ту же комету независимо друг от друга два или более наблюдателей. Именем кометы может стать название автоматической наблюдательной системы — все больше комет открывается с использованием орбитальных телескопов. Когда же комета теряется, но находится вновь — переоткрывается, к её имени добавляется имя астронома, который её переоткрыл. То есть, фактически меняется имя кометы — она будто становится новой в той или иной степени, — другой. И часто это именно из-за того, что она сменила орбиту. Другая орбита — другое имя, другой небесный объект... хотя физически это может быть всё та же ледяная глыба.

Удивительно, не правда ли?!

Бывает, что небесное тело гибнет. Кометы сталкиваются с планетами. Несколько таких случаев астрономы наблюдали непосредственно, и даже предвычисляли их. Самым ярким примером можно считать падение кометы "Шумейкеров — Леви 9" на Юпитер. Это случилось в 1994 году, и кометы этой уже в природе не существует, а орбита её есть — некоторая траектория в пространстве, по которой в некоторое время двигалась комета. И это с трудом поддается осознанию: "Как орбита может существовать отдельно от небесного тела?!"

Падение кометы "Шумейкеров — Леви 9" на Юпитер. Рисунок художника

Давайте представим, что у наших далеких потомков появятся технологии, позволяющие отбуксировать некоторую планету на другую орбиту. Возможно, когда-то придется подобное применить и к нашей Земле, ведь Солнце с течением времени будет разогреваться всё сильнее, что сделает условия вблизи прежней орбиты непригодными для жизни.

Можно ли будет считать отбуксированное на другую орбиту небесное тело той же планетой, называть его тем же именем?

Это — вопрос соглашения. Как люди решат, так и будет. Но важно понимать, что именно современная орбита Земли делает условия на её поверхности приемлемыми для нас. Будь наша планета чуть ближе к Солнцу, или немного дальше от него, всё на её поверхности было бы иным — другой состав атмосферы, другой температурный режим, другая продолжительность суток, ведь тогда и Луны могло бы у нас не быть, а Луна во многом определяет современный период обращения Земли вокруг оси.

Та ли это будет планета? — совершенно иная!

Посмотрите на Венеру — на первый взгляд это "сестра Земли", но условия, царящие на её поверхности, делают невозможным существование близких к нашей форм жизни.

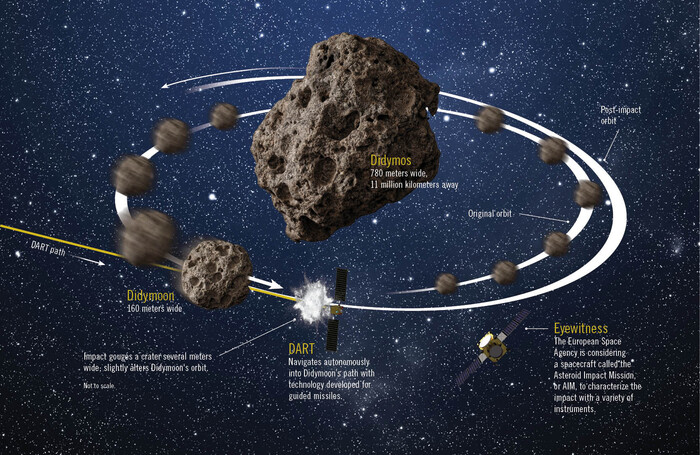
К слову о намеренном изменении орбит небесных тел — это не такая уж и фантастика. И в самом ближайшем будущем людям придется корректировать орбиты некоторых астероидов, чтобы избежать столкновения с ними. А какие-то малые планеты вполне можно разобрать на запчасти, используя их минеральную базу для строительства орбитальных поселений — космических городов, которые будут жить своей отдельной жизнью на своих собственных орбитах.

Недавно состоявшаяся коррекция орбиты системы двух гравитационно связанных астероидов "Дидим-Диморф"

В завершении рискну обратить Ваше внимание на философский аспект, имеющий параллель с нашей жизнью. Орбиту небесного тела можно уподобить линии его судьбы. Можно верить в судьбу или отрицать её как нечто предопределенное. Сейчас это не столь важно. Важно то, что судьба человека, его путь определяется не тем, как он выглядит, а тем, какие поступки он совершает. Именно это для людей первостепенно по важности. И часто бывает так, что если человек коренным образом меняет свою жизнь — начинает совершать другие по характеру поступки, кардинально меняется его окружение — его теряют из виду те, кто знал его прежде, а если даже встречают случайно, то не узнают — он как бы по другой орбите движется, на которой его никто уже не ожидает встретить.

И еще очень частое событие: Изменивший привычный ранее ход жизни человек скоро приходит к тому, что меняет и имя. Это может быть реальная смена имени и фамилии в паспорте, а может быть принятие творческого псевдонима. Но если изменения орбиты существенны, они с высокой вероятностью влекут за собой смену имени даже в мире людей. И это очень роднит небесное и земное. Иногда понимание этого помогает принять правильное сильное решение.

Автономный космический город будущего. Рисунок художника. Автор Samuel Nordius

Источник: NEANE Records

«Если вы меня спросите, зачем я занимаюсь небесной механикой, я отвечу: «Потому, что это полезно, это нужно людям».

Что такое современная небесная механика и для чего она нужна? Какие проблемы и задачи она может решить? Какие изобретения и приборы сделаны с её помощью? Каким образом она помогает делать открытия в других областях науки, и как связаны астрономия, небесная механика и современная техника?
Рассказывает Николай Владимирович Емельянов, доктор физико-математических наук, заведующий отделом небесной механики Государственного астрономического института имени П. К. Штернберга.

ВКонтакте: https://vk.com/video-190320587_456240117

Давайте представим, что нам нужно запустить футбольный мяч на орбиту Земли. Никакие ракеты не нужны! Хватит горы, высотой 100 километров и недюжинной силы. Но насколько сильно нужно пнуть мяч, чтобы он никогда больше не вернулся на Землю? Как отправить мяч в путешествие к звёздам, имея только грубую силу и знание небесной механики?

Сегодня в программе:

Бесконечные возможности одной формулы

Как взять энергию у Юпитера

Откуда у планет берутся кольца

Как математика помогла открыть Нептун

Благо, мы живём в век компьютерных технологий. Нам не нужно забираться на высокую гору и пинать мяч со всей силы, всё можно смоделировать! Давайте приступим.

Одна формула

Та самая, известная с уроков физики и астрономии:

Показывает, насколько сильно будут взаимодействовать тела, в зависимости от их масс, расстояния между ними и гравитационной постоянной G.

Я написал программу, в которой можно расставлять шарики, взаимодействующие друг с другом силами гравитации, при этом у каждого шарика есть своя масса, скорость и координаты. Для наглядности шарики оставляют за собой след.

Давайте поставим большой и массивный голубой шар(Землю) и маленький красный мячик недалеко от него. Запускаем симуляцию:

Он упал!

Для выхода на орбиту нужна скорость, чтобы шарик падал и все время промахивался мимо Земли. Но КАКАЯ скорость? И снова школьные знания приходят на помощь:

Минимальная скорость, необходимая для выхода на орбиту Земли называется первой космической скоростью.

Для Земли она равна 7.91 км/с. А для симуляции её можно легко вычислить:

Разгоняем мячик и смотрим результат

Полёт нормальный!

Шарик описывает окружность с Землёй в центре. Что будет, если придать ему чуть больше скорости? Сейчас проверим:

Теперь форма орбиты эллиптическая, можно выделить 2 очень важные точки — апогей и перигей.

Апогей — это точка, в которой мячик максимально удалён от Земли.

Перигей — наоборот, самая близкая к Земле точка.

При увеличении начальной скорости перигей не меняется, а вот апогей становится всё дальше, и в конце концов имеет бесконечное расстояние до Земли. Тут мы вплотную приблизились к понятию второй космической скорости. Это скорость, которую надо придать шарику, чтобы он преодолел гравитацию Земли и улетел бороздить просторы вселенной. Для земли она равна 11.2 км/с.

Интересный фокус: если мы умножим первую космическую скорость на √2, то получим вторую космическую.

Умножили. Запустили. Получили:

Он улетел безвозвратно! Кстати, теперь он имеет параболическую орбиту. А если запустить шарик ещё сильнее, получим гиперболу. Интересно получается, везде нас преследует математика.

При этом формула остаётся всё той же. Окружность превращается в эллипс, эллипс в параболу, а парабола в гиперболу из-за вытягивания орбиты(увеличения эксцентриситета).

Как взять энергию у Юпитера?

Давайте расширим нашу модель, добавим Солнце, заставим Землю крутиться вокруг него.

Представим, что мячу нужно придать такую скорость, чтобы он улетел за пределы Солнечной системы — третью космическую скорость. В реальном мире она равна 16.7 км/с. К сожалению, эта скорость слишком большая, боюсь, нам не хватит сил…

Постойте! А что, если забрать немного скорости у какого-нибудь массивного тела, например, Юпитера. Мы можем подлететь к чему-то очень массивному и совершить гравитационный манёвр. При пролёте мимо Юпитера силы гравитации взаимно притягивают мячик и газовый гигант, но масса мячика настолько мала, что почти никак не влияет на движение Юпитера, а сам Юпитер разгоняет пролетающее мимо тело до высоких скоростей.

Меньше слов — больше дела:

Момент гравитационного манёвра — шарик подлетел к Юпитеру.

Ура! Мы получили скорость, достаточную для выхода из Солнечной системы, при этом ничего не потратили. Правда, Юпитер стал двигаться чуть медленнее, но мы этого точно не заметим.

Все космические аппараты, запущенные человеком за пределы солнечной системы («Вояджеры» 1 и 2, «Пионеры» 10 и 11, «Новые горизонты») использовали именно такой способ для ускорения.

Увеличиваем масштаб!

Я добавил трение частиц, чтобы, сталкиваясь, они передавали часть энергии друг другу. Также я ввёл силу нормальной реакции, теперь частицы уважают своё личное пространство, отталкивая от себя других.

Поставим случайную генерацию шариков и зададим им случайное направление и скорость. Пусть их будет, допустим, 100 штук.

Полный хаос, каждая частица движется куда хочет, но всё же силы гравитации берут своё, и начинают образовываться скопления шариков:

И через некоторое время получается большое тело, состоящее из 99 шариков и один-единственный шарик, обращающийся вокруг него:

При другом запуске получилось следующее:

Два массивных тела, обращающихся вокруг общего центра масс. Если представить, что эти два объекта — звёзды, то мы получили двойную звезду. Интересно, что примерно половина звёзд в нашей галактике — двойные. Если бы у нашего Солнца была звезда — компаньон, то в небе мы могли бы наблюдать такую картину:

Откуда у планет берутся кольца?

Основная причина появления колец — это разрушение спутников, подлетевших слишком близко к планете, а точнее, пересёкших предел Роша. В таком случае приливные силы, вызываемые гравитацией планеты, становятся больше сил, удерживающих спутник целым, и он разрывается на много частей, оставляя после себя кольцо, которое опоясывает планету. Давайте смоделируем эту ситуацию:

Спутник чуть дальше предела Роша, он вращается вокруг планеты по стабильной круговой орбите. Но что будет, если сгенерировать его чуть-чуть ближе к планете?

Спутник разлетелся на множество маленьких частей, которые образовали кольца вокруг планеты. Так же и в реальном мире. Тритон (спутник Нептуна) постепенно приближается к планете, и через 2 миллиарда лет будет разорван, а у Нептуна появятся кольца больше, чем у Сатурна.

Как открыли Нептун и при чём здесь математика?

Раз уж зашла речь о Нептуне, давайте поговорим о его открытии. «Планета, открытая на кончике пера» имеет массу, а значит, действует на объекты вокруг. Астрономы 19 века заметили изменения в орбите Урана, его орбита отличалась от расчётной, видимо, что-то влияло на него. Орбита Урана имела возмущения:

Это утрированная модель показывает, как неизвестное тело за Ураном влияло на его орбиту. Астрономам оставалось только вычислить положение тайной планеты и посмотреть в телескоп. Действительно, планета Нептун оказалась именно там, где её и предсказывали!

Заключение

Конечно, эта симуляция не обобщает все законы и явления, происходящие в космосе, например, здесь не учитывается теория относительности Эйнштейна, так как скорость частиц далека от скорости света. Но есть ещё много интересных вещей, которые можно реализовать в этой симуляции. Попробуйте сами! Понадобится только Python3 и библиотека Pygame.

https://habr.com/ru/post/494546/