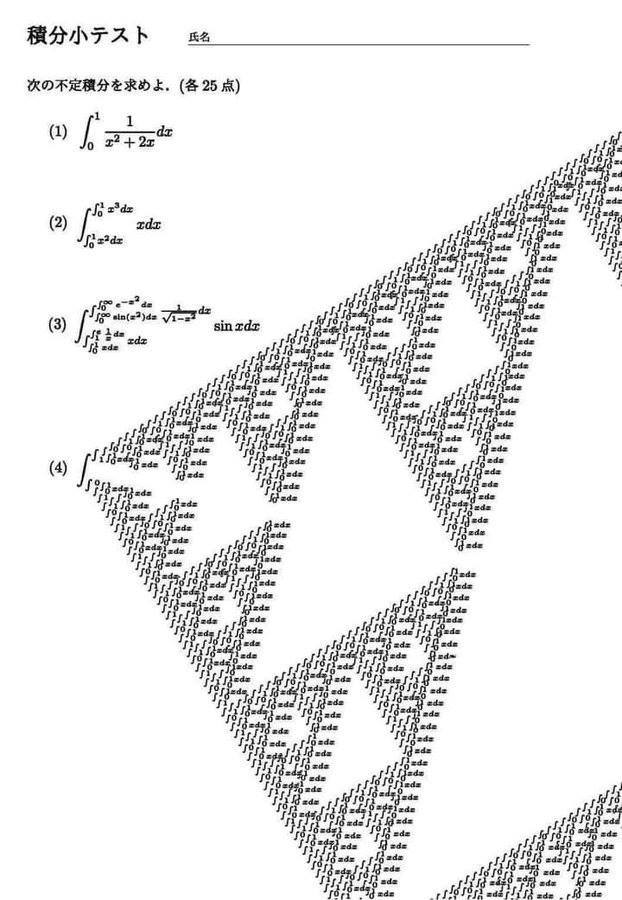
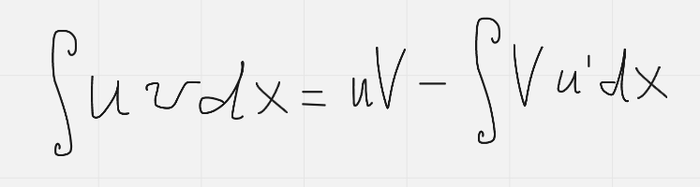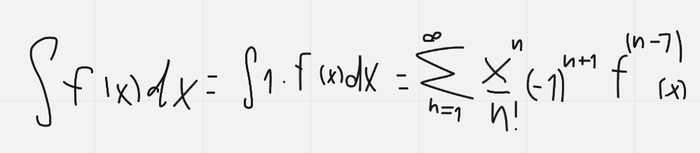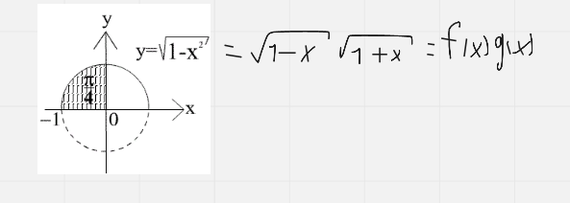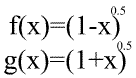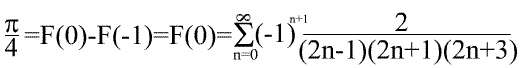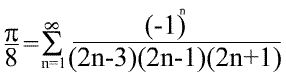Что такое ПРЕДЕЛЫ. Математика на QWERTY
Вместе с математиком Георгием Вольфсоном мы сделали цикл роликов "А на хрена нам ___ ?". В комментариях выпуска про интегралы было много пожеланий рассказать про пределы. В новом ролике постарались рассказать об этом простыми словами.
Содержание ролика:
00:21 Парадоксе об Ахиллесе и черепахе. Парадокс Зенона.
03:49 Предел последовательности
04:30 Предел на графике
05:42 Бессчетное множество половин
06:25 Сколько нужно бросков игральных костей для теории вероятности
08:05 Предел функции
09:25 Замечательный предел
11:00 Может ли быть такое, что предела нет?
Если стало интересно, то вот и предыдущий ролик про интегралы:
Новый вид объявлений1
Сегодня после прогулки с собакой увидел у подъезда вот такое объявление. Интересно, кто то вспомнил про задание на лето или реально готовы платить за какие то примеры)
Интеграл произведения. Продолжение
Получаем
Интеграл справа по этой же формуле раскрываем до бесконечности, тогда...
Здесь Vn+1 это интеграл (n+1)го порядка. Эта формула и будет нашим главным объектом исследований. Проверим её работоспособность например так:
Или так:
Этот ряд в конце равен 1, всё сходится. Таким способом можно вообще получать новые ряды.
Любую функцию можно представить как единица умноженная на её саму и применять нашу формулу.
Переобозначим, пусть F(x) это интеграл от f(x), тогда вообще похоже на ряд Тейлора получается:
Это разложение называется асимптотическим. Возможно, это проходят на мехмате, но я это получил до вуза, потом учился на физфаке и сейчас ничего более по этому поводу сказать, к сожалению, не могу.
====================================================================================
А теперь получим ряд для числа Пи:
В википедии среди множества других рядов такого ряда я не нашёл.)
Мою старую писанину с обозначением стрелочки вверх, как интеграл, можно скачать здесь https://project.1sept.ru/works/586753
Как дифференциальные уравнения помогают понять работу клеток головного мозга
Чтобы понять, как работает человеческий мозг, недостаточно усилий одних только биологов. Нейроны работают с помощью, в том числе, электрических сигналов, а значит, можно построить электрическую схему отдельно взятого нейрона и описать ее математически. И здесь нам снова понадобятся дифференциальные уравнения — системы уравнений Фитцхью-Нагумо.
Термин «вычислительная нейробиология» (computational neuroscience) появился совсем недавно — в 1985 году его предложил профессор Бостонского университета Эрик Шварц (Eric Schwartz), и это как раз та ситуация, когда наука появилась намного раньше — в середине XX века, — чем ее название.
К тому моменту ученым уже давно было известно, что мозг и нервная система построены из электрически возбудимых клеток — нейронов, предназначенных для приема извне, обработки, хранения, передачи и вывода вовне информации с помощью электрических и химических сигналов. Нейроны могут соединяться один с другим, формируя сети; в головном мозге человека насчитывается около 90–95 миллиардов нейронов.
Описать работу нейронов проще всего через математические системы с заданными параметрами. Этим и занимаются ученые, работающие в области вычислительной нейробиологии, с помощью моделей, предложенных математиками почти семьдесят лет назад.
источник https://nplus1.ru/material/2020/02/19/fitzhugh-nagumo-model?...