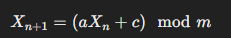Случайность в играх: математические алгоритмы, которые оживляют игровой мир⁠⁠

Случайность – неотъемлемый элемент современного игрового процесса. От распределения лута до генерации уровней – случайные события влияют на динамику, баланс и реиграбельность. Ниже рассмотрены ключевые подходы к реализации случайности, математические основы и наиболее популярные алгоритмы.

Применение случайности в играх

Генерация контента. Процедурное создание карт, уровней и миссий позволяет разработчикам создавать бесконечное множество уникальных сценариев.
Игровая механика. Распределение лута, шанс на критический удар, поведение AI – все эти элементы зависят от качественного рандома.
Баланс и динамика. Случайные события помогают избежать предсказуемости, делая игровой процесс более захватывающим и адаптивным к стилю игрока.

Математическая природа случайности

Большинство игр используют так называемые псевдослучайные числа, которые генерируются с помощью специальных алгоритмов. В отличие от настоящей случайности, которая требует использования внешних источников хаоса (например, шумов или физических процессов), псевдослучайные числа создаются детерминированными программными методами. Это значит, что если задать одинаковое начальное значение (seed), алгоритм всегда выдаст одну и ту же последовательность чисел. Такая воспроизводимость крайне полезна для тестирования и отладки игр, а также для синхронизации событий в мультиплеерных сессиях, где важно, чтобы все игроки видели одинаковые результаты случайных процессов.

Алгоритмы генерации случайных чисел

Линейный конгруэнтный генератор (LCG)

LCG – один из самых простых и быстрых алгоритмов для генерации псевдослучайных чисел. Он работает по следующей формуле:

Как работает LCG

Инициализация:
Алгоритм начинается с исходного числа (X0), которое выбирается как seed.
Рекурсия:
На каждом шаге вычисляется новое значение по формуле. Операция взятия по модулю гарантирует, что результат всегда остаётся в пределах заданного диапазона.
Генерация последовательности:
Процесс повторяется, и получается последовательность чисел, которая кажется случайной, если смотреть на отдельные значения.

Преимущества LCG

Простота реализации:
Алгоритм требует минимального объёма кода и легко реализуется практически на любом языке программирования. Зачастую стандартная библиотека Random реализует именно такой подход
Высокая скорость:
Основные операции (умножение, сложение, операция по модулю) выполняются очень быстро, что делает алгоритм подходящим для задач, где важна производительность.

Недостатки и ограничения

Короткий период повторения:
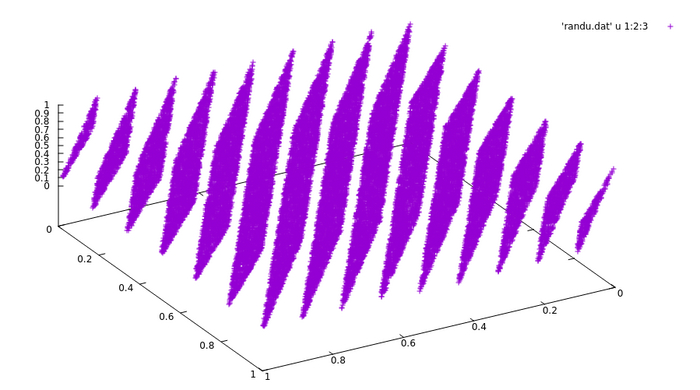
Поскольку множество возможных состояний ограничено (от 0 до m−1), последовательность рано или поздно начинает повторяться. При неправильном выборе параметров период может быть слишком коротким, что приводит к предсказуемости.
Корреляция между значениями:
Сгенерированные числа могут быть статистически зависимыми. Это особенно заметно при использовании LCG для многомерного моделирования, где точки могут выстраиваться в определённые шаблоны или линии, а не распределяться равномерно.

Чувствительность к параметрам:
Чтобы достичь максимально возможного периода и хорошего качества случайности, необходимо тщательно подбирать значения m, a и c. Неправильная комбинация может привести к существенным искажениям в распределении чисел.
Ограниченность для сложных задач:
Для задач, где качество случайности критично (например, в криптографии, симуляциях физических процессов или азартных играх), LCG не подходит. Его предсказуемость и недостаточная сложность могут стать уязвимостью или привести к неверным результатам.
Опасность взлома:
LCG достаточно просто взломать, всего по первым 3-5 числам, а если увеличить количество входных данных, то это можно будет сделать даже на стареньком ноуте.

Mersenne Twister

Один из самых популярных алгоритмов в разработке игр. Он обладает чрезвычайно длинным периодом (2¹⁹⁹³⁷ − 1) и обеспечивает равномерное распределение. Благодаря сбалансированному соотношению между качеством и скоростью, Mersenne Twister применяется во многих игровых движках.

Как работает алгоритм

Массив состояний:
Алгоритм использует внутренний массив из 624 целочисленных значений, который представляет текущее состояние генератора. При каждом обновлении этого массива используются значения предыдущих элементов для вычисления новых.
Рекуррентное обновление:
Новый элемент состояния вычисляется с помощью линейной рекурсии, где используются битовые операции. Эта стадия обеспечивает быстрый переход от одного состояния к другому, что позволяет быстро генерировать большое количество чисел.
Процесс "темперирования":
После обновления состояния полученные числа проходят через серию битовых преобразований – так называемый процесс темперирования. Эти операции (битовые сдвиги, XOR и маскирование) устраняют возможные корреляции между соседними числами, обеспечивая равномерное распределение по всему диапазону.

Основные преимущества

Чрезвычайно длинный период:
С периодом в 219937−12^{19937} - 1219937−1 последовательность чисел повторяется настолько редко, что для большинства практических задач в играх повторение практически не происходит.
Равномерное распределение:
Алгоритм гарантирует равномерное распределение чисел в 623 измерениях, что критически важно для симуляций, процедурной генерации уровней и других аспектов игрового дизайна.
Баланс между скоростью и качеством:
Благодаря оптимизации операций на битовом уровне, Mersenne Twister способен быстро генерировать случайные числа без ущерба для их статистического качества. Это делает его идеальным для игровых движков, где производительность имеет решающее значение.

Ограничения

Не для криптографии:
Хотя алгоритм отлично справляется с задачами общего назначения, его не следует использовать там, где требуется криптографическая стойкость. При наличии достаточных данных о состоянии генератора, его последовательность можно предсказать.
Потребление памяти:
Использование массива из 624 чисел может быть незначительной проблемой в большинстве игр, но для встроенных систем с ограниченными ресурсами это может стать важным фактором.

XORShift

XORShift – это алгоритм генерации псевдослучайных чисел, который основан исключительно на битовых операциях: XOR (исключающее ИЛИ) и битовых сдвигах. Его простота и эффективность делают его привлекательным для задач, где критична производительность.

Основной принцип работы

Инициализация состояния:
Алгоритм использует внутреннее целочисленное состояние (или набор состояний), которое инициализируется исходным значением (seed). Это состояние будет преобразовываться на каждом шаге.
Битовые операции:
Основная идея заключается в последовательном применении битовых сдвигов и операции XOR. Простой пример для 32-битного числа может выглядеть так:
x ^= x << a;
x ^= x >> b;
x ^= x << c;
Здесь a, b и c – подобранные константы, которые определяют, насколько сильно будут перемешаны биты. Эти операции изменяют состояние так, что полученное число кажется случайным.
Обновление состояния:
После выполнения этих операций новое состояние используется для генерации следующего числа. Весь процесс повторяется, создавая последовательность псевдослучайных чисел.

Преимущества XORShift

Высокая скорость:
Битовые операции выполняются крайне быстро на современных процессорах, что делает алгоритм одним из самых производительных.

Ограничения и недостатки

Качество случайности:
Хотя XORShift хорошо справляется с генерацией числовых последовательностей, его статистическая "случайность" может уступать более сложным алгоритмам. В некоторых случаях последовательности могут иметь выявляемые закономерности или корреляции, особенно в многомерном пространстве.
Непригодность для критичных задач:
Для задач, требующих высочайшего качества случайных чисел, XORShift может оказаться недостаточно надёжным.
Вариативность реализации:
Существует множество вариантов алгоритма XORShift, и выбор конкретных констант (a, b, c) существенно влияет на качество выходной последовательности. Неправильный подбор параметров может привести к сокращению периода генератора или к появлению предсказуемых шаблонов.

PCG (Permuted Congruential Generator)

PCG – это относительно современный алгоритм генерации псевдослучайных чисел, который объединяет простоту линейного конгруэнтного метода с дополнительным этапом перестановки битов для улучшения качества результата.

Основной принцип работы

Базовый этап (LCG):
Алгоритм начинается с применения линейного конгруэнтного генератора, где новое состояние вычисляется по формуле приведенной в пунтке про LCG
Этап перестановки битов:
Вместо того чтобы напрямую использовать число, полученное на базовом этапе, к нему применяется функция перестановки XOR.

Преимущества PCG

Высокое качество случайности:
Перестановка битов значительно улучшает статистические характеристики выходной последовательности.
Быстродействие:
Используемые арифметические и побитовые операции выполняются очень быстро, что позволяет генерировать случайные числа в режиме реального времени, не замедляя работу игры.
Экономия памяти:
В отличие от некоторых более сложных алгоритмов, PCG требует относительно небольшого объёма памяти, что делает его оптимальным выбором для мобильных игр и встроенных систем с ограниченными ресурсами.

Недостатки PCG

Сложность реализации:
В отличие от простых LCG, PCG включает дополнительный этап перестановки битов, что делает его реализацию более сложной. Это может затруднить отладку и понимание внутренней работы генератора для новичков.
Относительно небольшая база практического опыта:
Несмотря на положительные результаты тестирования, PCG – сравнительно новый алгоритм. Его применение в долгосрочных проектах и в условиях экстремальной нагрузки может выявить скрытые недостатки, которые пока менее изучены по сравнению с более зрелыми генераторами, такими как Mersenne Twister.
Не подходит для криптографических целей:
Как и большинство PRNG, PCG не обеспечивает криптографическую стойкость.

Криптографически безопасные генераторы (CSPRNG)

Используются в случаях, когда необходимо предотвратить предсказуемость исходов (например, в играх с денежными ставками или при обработке важных событий). Несмотря на их высокую степень энтропии, такие алгоритмы обычно работают медленнее и требуют дополнительных ресурсов.

Основные принципы работы

Использование криптографических примитивов:
CSPRNG базируются на проверенных криптографических алгоритмах, таких как блочные шифры (например, AES) или криптографические хеш-функции.

Преимущества использования CSPRNG

Высокая степень энтропии:
Такие генераторы обеспечивают практически «настоящую» случайность, что критически важно для предотвращения манипуляций и мошенничества. Например, в азартных играх.
Защита от предсказуемости:
Криптографические методы гарантируют, что даже при наличии некоторых данных о состоянии генератора, предсказать последующие числа практически невозможно. Это делает их незаменимыми в системах, где безопасность имеет первостепенное значение.

Недостатки и компромиссы

Скорость работы:
Из-за сложных криптографических операций, таких как шифрование и хеширование, CSPRNG обычно работают медленнее по сравнению с традиционными алгоритмами.
Потребление ресурсов:
Криптографически безопасные алгоритмы требуют больше вычислительных ресурсов для обеспечения высокого уровня безопасности.
Сложность реализации:
Реализация CSPRNG требует глубокого понимания криптографических принципов и тщательного тестирования, чтобы избежать ошибок, которые могут снизить уровень безопасности.

Аппаратные генераторы случайных чисел

Аппаратные генераторы случайных чисел (HRNG) основаны на физических процессах, которые по своей природе обладают истинной случайностью, в отличие от алгоритмических (псевдо) генераторов. Ниже рассмотрим, как они работают, их преимущества и ограничения.

Принцип работы

Физическая основа:
В основе HRNG лежат процессы, происходящие в физическом мире, такие как тепловой шум в диодах, шум в резисторах, флуктуации в электрических цепях или квантовые эффекты. Например, при измерении шума диода регистрируется случайная величина, возникающая из-за колебаний заряда на уровне атомов. Аналогично, квантовые процессы, например, распад радиоактивных элементов или квантовая туннельная проводимость, дают истинно случайные результаты.
Конвертация в цифровой сигнал:
Полученные аналоговые сигналы преобразуются в цифровой формат с помощью аналого-цифровых преобразователей (ADC). Этот процесс позволяет использовать физическую случайность для генерации последовательности чисел, пригодной для программного применения.

Преимущества аппаратных генераторов

Истинная случайность:
Поскольку источники HRNG основаны на физических явлениях, генерируемые числа не являются предсказуемыми и не повторяются, что делает их идеальными для криптографических и высокозащищённых приложений.
Высокая энтропия:
Такие генераторы обладают высокой степенью случайности, что особенно важно в системах, где малейшая предсказуемость может привести к уязвимостям.

Ограничения и проблемы интеграции

Сложность аппаратной реализации:
Для работы HRNG требуется специализированное оборудование, которое должно точно измерять и обрабатывать физические сигналы. Это усложняет их интеграцию в стандартные игровые движки.
Стоимость и ресурсоемкость:
Создание и поддержка аппаратного генератора требует дополнительных затрат на оборудование, калибровку и периодическое обслуживание.
Скорость генерации:
Хотя физическая случайность обеспечивает высокий уровень энтропии, процесс преобразования аналогового сигнала в цифровой может быть медленнее по сравнению с алгоритмическими методами.

Выбор алгоритма: баланс между качеством и производительностью

При выборе алгоритма разработчикам необходимо учитывать:

Производительность. В реальном времени важна скорость генерации случайных чисел.
Качество случайности. Для игровых механик, влияющих на баланс, необходим алгоритм с минимальной корреляцией.
Воспроизводимость. Возможность регенерировать последовательности по заданному сиду полезна для отладки и синхронизации в мультиплеерных режимах.
Безопасность. Для критичных к предсказуемости систем (например, азартных игр) следует использовать CSPRNG.

Mersenne Twister остается золотым стандартом для большинства игр благодаря своему оптимальному сочетанию всех вышеперечисленных характеристик. Однако для специализированных задач все чаще применяются алгоритмы типа PCG или криптографически безопасные методы.

Заключение

Случайность в играх – это не просто имитация хаоса, а продуманный инструмент, основанный на математических принципах и алгоритмах. Правильный выбор метода генерации случайных чисел напрямую влияет на игровой баланс, производительность и опыт пользователя. Для разработчиков важно понимать сильные и слабые стороны каждого алгоритма, чтобы адаптировать решение под конкретные задачи проекта.

Подписывайся на телеграм канал нашей студии, там ещё больше механик, полезностей, историй и туториалов.