Как связаны кролики и Парфенон?
Люди повсюду используют математику, и даже сама природа ищет математические законы. Это пост о красивой константе, найденной и человеком, и эволюцией
В 12 веке родился Леонардо Пизанский. Он стал первым крупным европейским математиком. Именно он положил начало использованию позиционной системы счисления. Проще говоря, благодаря ему мы пишем числа удобными арабскими цифрами, а не длинными рядами римских. Сравните: MMXVIII и 2018
Вам этот математик может быть известен под именем Фибоначчи. Однажды, он поставил следующую задачу:
Некто приобрел пару новорождённых кроликов и поместил их в огороженный со всех сторон загон. Сколько пар кроликов будет через год, если считать, что каждый месяц пара дает в качестве приплода новую пару кроликов, которые со второго месяца жизни также начинают приносить приплод?
Попытаемся решить её! Так выглядят наши кролики в первый месяц — маленькие мальчик и девочка
Во второй месяц кролики подрастают
В третий рождается ещё одна пара — также мальчик и девочка. Из-за того, что тут происходит, назовём это семейство Таргариенами
В четвёртый месяц наши первоначальные кролики рождают ещё одну пару, а малыши Дейенерис и Визерис подрастают
Итак, сколько же пар кроликов будет через 12 месяцев? Допустим, что кролики живут в идеальных условиях — не стареют, не погибают и не свергаются другой династией
Взрослых кроликов будет столько же, сколько всего кроликов было на предыдущем шаге: так как взрослые останутся, а малыши подрастут. Запишем это:
взрослые[n] = кролики[n-1]
Детей же в новом месяцу будет столько же, сколько было взрослых в прошлом. А их, как говорит формула выше, — столько же, сколько кроликов всего в позапрошлом!
дети[n] = взрослые[n-1] = кролики[n-2]
Получаем итоговую формулу: кроликов в этом месяце будет столько, сколько их было вместе в предыдущие 2 месяца:
кролики[n] = кролики[n-1] + кролики[n-2]
То есть, нашу последовательность можно продлить на сколько угодно месяцев вперёд! Получим 1 1 2 3 5 8 13 21… Это называется последовательностью Фибоначчи. Сможете ли вы теперь дать ответ на задачу?
Красота последовательности
Оказалось, что этот ряд чисел, найденный при помощи такой абстрактной задачи, обладает очень интересными свойствами! Несмотря на то, что кролики в реальной жизни ведут себя не так, эта последовательность присутствует в природе повсюду
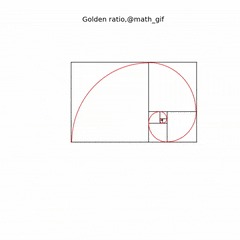
Стороны прямоугольника — это числа Фибоначчи
Вот одно из её свойств. Отношение соседних чисел в ней назвали золотым соотношением. Соседние числа относятся друг к другу одинаково (чем дальше, тем точнее это приближается к одному числу, равному 1,618).
Считается, что «золотые пропорции» лучше и приятнее воспринимаются человеком. Парфенон строился с множеством архитектурных ухищрений так, чтобы выглядеть наиболее приятно. Одним из таких приёмов считается золотое сечение:
Но самые прекрасные примеры золотого соотношения можно найти в природе. Например, раковины моллюков:
Такая форма наиболее выгодна и выработалась эволюционно. Разберём, почему это так и ещё одно свойство золотого отношения на моём любимом примере
Растения
Представьте себя растением. Надеюсь, вам в голову пришёл могучий дуб, но для этого примера лучше представить цветок или, скажем, спиральный алоэ
Предположим, вам только предстоит вырастить листья. Будучи очень умным алоэ, вы хотите расположить их максимально эффективно. Единственный параметр, который вам доступен — это угол, на который можно повернуть следующий лист
Разберём на примере. Первый лист можно расположить, где угодно
Предположим, выбран угол поворота 180 градусов. Или, более просто — половина окружности, ½. Тогда второй лист будет напротив. Третий — на месте первого и так далее
Если вы хотите быть конкурентоспособным растением, а не обнимашек, то кажется, это не самый эффективный способ. Может быть попробовать 1/3 окружности?
Тогда будет 3 «пика» и возможность вдохновить братьев Райт.
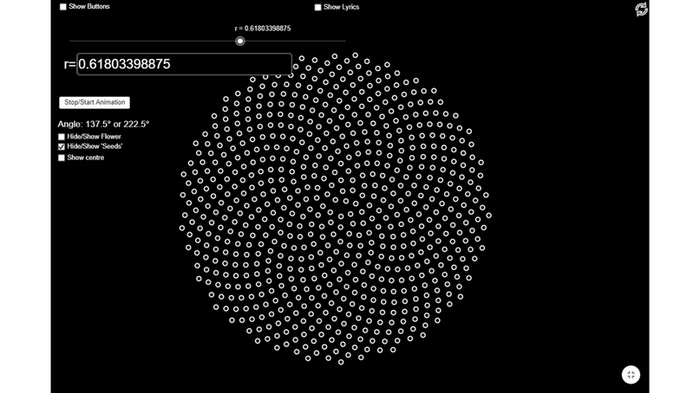
Но похоже, что число пиков равно знаменателю дроби! Растение, знакомое с математикой, могло бы сказать, что тогда выгоднее всего использовать иррациональное число — которое нельзя представить в виде дроби. Таким числом и является золотое соотношение φ! А самым выгодным оказывается угол поворота 1/φ. Так будет выглядеть распределение листов, использующее золотое соотношение:
А так выглядит реальное растение!
Можно поиграть с симуляцией самостоятельно
Если нравятся посты о науке и учёбе, заглядывайте ко мне в ВК и телеграм
















Лига образования
4.4K поста21.8K подписчиков
Правила сообщества
Публиковать могут пользователи с любым рейтингом. Однако мы хотим, чтобы соблюдались следующие условия:
ДЛЯ АВТОРОВ:
Приветствуются:
-уважение к читателю и открытость
-желание учиться
Не рекомендуются:
-публикация недостоверной информации
ДЛЯ ЧИТАТЕЛЕЙ:
Приветствуются:
-конструктивные дискуссии на тему постов
Не рекомендуются:
-личные оскорбления и провокации
-неподкрепленные фактами утверждения
В этом сообществе мы все союзники - мы все хотим учиться! :)