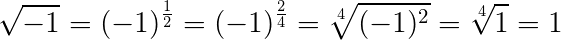Что-то тут нечисто
P.S. Может оказаться баяном, но вроде не встречал на сайте.
Раз уж ты оперируешь мнимой единицей, будь добр указывать всё множество корней из комплексного числа.
раскрыть ветку (7)
Я не успел отредактировать комментарий, так что напишу так.
Если кому интересно, здесь ошибка в переходе (-1)^(1/2)=root4((-1)^2)
Суть в том, что у первого выражения множество из двух ответов, а у второго - из четырёх.
Корректный переход мог бы быть (-1)^(1/2)=(root4(-1))^2
раскрыть ветку (6)
Я вижу, что тождество нарушено на этапе (-1)^(2/4) = sqrt4((-1)^2), но не могу формально объяснить, в чем ошибка. Указывая изменение числа корней, вы констатируете ошибку, а не объясняете ее.
раскрыть ветку (5)
Хорошо, тогда так: порядок действий в (-1)^(2/4) не определён, можно сначала взять квадрат, а потом корень, а можно сначала корень, потом квадрат. В первом случае будет не равенство, а включение множества, во втором случае множество решений не изменится.
раскрыть ветку (4)
Я вижу. Но как формально объяснить, что выражение a^(b/c) можно раскрывать как a^(1/c)^b, но нельзя a^b^(1/c)? Какое правило символьных преобразований я нарушу?
раскрыть ветку (3)
Если мне маразм не изменяет, по определению рациональный показатель степени раскрывается как a^(b/c) = (a^(1/c))^b. А раскрытие в другом порядке допустимо, только если дробь несократима.
Определение принято таким, потому что только в этом случае количество корней не изменится независимо от того, была ли сначала сокращена дробь, или дробная степень была представлена в виде степени корня.
раскрыть ветку (1)
Не, вру. То определение для вещественных положительных чисел a. По определению для комплексных чисел a^b = e^(b*lna). Таким образом, a^(b/c) =e^(b/c*lna) = e^(b/c*(Lna+2πin)) = e^(b/c*Lna+b/c*2πin)). То есть, чтобы найти количество значений этого выражения, нужно найти количество различных значений числа bn/c по модулю 1, где n∈ℤ. Если обозначить b=kp, c=kq, где k=НОД(b,c), получим q значений.
Если мы хотим это сравнить с (a^b)^(1/c), то должны раскрыть это по тому же правилу: (a^b)^(1/c) = e^(1/c*ln(a^b)) = e^(1/c*ln(e^(b*lna))) = e^(1/c*(Ln(e^(b*lna))+2πin)) = e^(1/c*(b*lna+2πin)) = e^(1/c*(b*(Lna+2πim)+2πin)) = e^(1/c*b*(Lna+2πim)+1/c*2πin) = e^(b/c*Lna+b/c*2πim+1/c*2πin) = e^(b/c*Lna+1/c*2πi(b*m+n)). Здесь аналогично: нужно найти количество различных значений числа (bm+n)/c по модулю 1, где n,m∈ℤ. Однако здесь уже числитель - это произвольное целое, а не кратное b, как было выше. Значит, количество значений равно c.
Можно расписать еще (a^(1/c))^b, чтобы убедиться. (a^(1/c))^b = e^(b*ln(a^(1/c))) = e^(b*ln(e^(1/c*lna))) = e^(b*(Ln(e^(1/c*lna))+2πin)) =
e^(b*(1/c*lna+2πin)) = e^(b*(1/c*(Lna+2πim)+2πin)) = e^(b/c*(Lna+2πim)+b*2πin) = e^(b/c*Lna+b/c*2πim+b*2πin) = e^(b/c*Lna+b*2πi(1/c*m+n)). Здесь это число b(1/c*m+n) = b(m+cn)/c, n,m∈ℤ. Здесь так же можно сократить b и c, и получить q=c/НОД(b,c) значений.
Впрочем, как и ожидалось, результат тот же. Но доказал по правильному определению и более строго, что a^(b/c) = (a^(1/c))^b ≠ (a^b)^(1/c) для a∈ℂ, b∈ℕ, c∈ℤ.